The conventional supervised machine learning (ML) workflow, partly discussed in a recently published article in DSDE, has been around for over 4 decades. It basically involves creating a single instance of a certain ML method. The supervised ML workflow accepts a training set of data, builds a model, optimizes the model parameters, and uses the trained model to predict the target variable from a new set of input data.
Details on the ML concept specifically and the artificial intelligence (AI) technology in general were published in TWA last year. In essence, there is only one “recommended” solution to the targeted prediction problem in the conventional supervised learning workflow. There is no alternative recommendation except to conduct another run with a different set of model parameters or apply another single-instance ML method on the same data. This way, we simply get another recommended solution from another instance or method. There is no efficient way to combine the individual solutions for more robust decision making.
The hybrid ML methods are similarly based on a single instance, and therefore, provide a single solution to a problem. What if we could generate a number of “possible solutions” to the same problem? What if we could generate a “committee of candidate solutions” to the same problem? We would then combine them in a way to evolve a single robust solution.
In fact, we can. We already have the method.
The concept is called “ensemble machine learning (EML).” If you have used the random forest algorithm, then you already have used the EML method, probably without realizing it. This article will explain, in very simple terms, the principle behind this relatively new ML paradigm.
What is EML?
The EML method creates multiple instances of traditional ML methods and combines them to evolve a single optimal solution to a problem. This approach is capable of producing better predictive models compared to the traditional approach. The top reasons to employ the EML method include situations where there are uncertainties in data representation, solution objectives, modeling techniques, or the existence of random initial seeds in a model. The instances or candidate methods are called base learners. Each base learner works independently as a traditional ML method, and the eventual results are combined to produce a single robust output. The combination could be done using any of the averaging (simple or weighted) methods and voting (majority or weighted) for regression and classification methods, respectively.
EML methods are also known as “committee of machines” or “committee of experts” with the latter following the assumption that each base learner is an “expert” and its output is an “expert opinion.”
An illustration of the EML method is shown in Fig. 1. The first layer comprising classifiers 1, 2, and 3 could be composed of different instances of the same traditional ML method or simply different ML methods. They may process the same data but with different model parameters. They may also use different bootstrap samples of the same data with the same model parameters. Bootstrapping is a resampling technique used to estimate statistics on a population by sampling a data set with a replacement. This ensures that the output of each base learner is slightly different with varying degrees of diversity.
The second layer shows the combination of the results of the base learners. A relevant algorithm such as simple averaging or majority voting can be applied on the combined results. The third layer shows the ensemble result of the combination algorithm to evolve a single robust output. It has been reported (Dietterich, 2000) that such EML outputs are more accurate than the results of the individual classifiers.
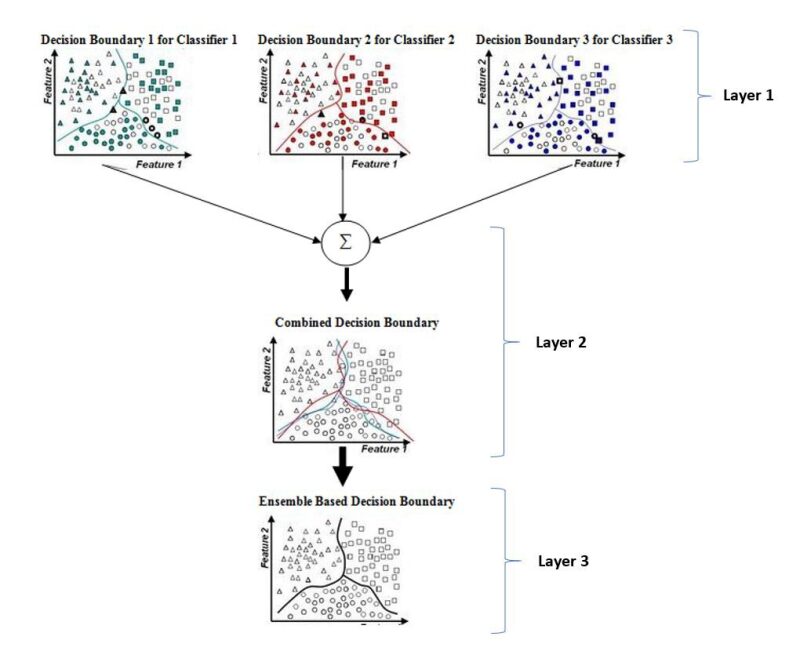
Justification for the EML
The EML is an emulation of the human social learning behavior of seeking multiple opinions before making a decision. In human psychology, the judgment of a committee is believed to be superior to and more trusted than that of individuals. The major motivation for the EML method is the statistically sound argument that it is part of human strategies for decision making. Some examples of the human strategies for decision making:
- We ask for a “second opinion” from several doctors before undergoing a medical or surgical procedure.
- We visit several showrooms or read reviews of different brands before buying a new vehicle.
- Journal editors seek the opinions of reviewers before deciding whether to accept a manuscript. (In fact, several reviewers read this article and their suggestions were implemented to evolve the final version.)
Such examples are almost endless. In each case, the main objective is to minimize the likelihood of error in the final decision, or in this case the EML decision. We usually do not consider taking such “ensemble” decisions as a mistake. Even when such decisions lead to negative outcomes, we do not usually regret it as we deem them “informed” decisions. The same assumptions go into the results of EML methods.
Diversity: A Major Requirement for EML
The existence of diversity is the major requirement for the implementation of an EML method. The EML model should be built in such a way that the outputs of the base learners are diverse. This is to mimic the divergent opinions of members of a committee in the human case. An issue needs to be thorny and knotty to require a committee to help make a decision. If all the members of a committee always agree on all issues, then there is no need to have the committee in the first place. An individual’s opinion would be just as good. The same applies to the EML method. If the base learners are too homogenous, such that they all produce the same result, then the desired objective will not be achieved.
Diversity can be created in a problem from the data or model perspective. Different bootstrap samples can be extracted from the same data. Since different tuning parameters produce different outputs from a model, such could be used as the basis to create diversity in the base learners.
Types of EML
The most common types of EML methods are bagging, boosting, and stacking. Bagging is an acronym derived from bootstrap aggregation. It involves taking several random subsamples of the original data with a replacement. Each base learner is trained independently on a subsample of data, and the trained learner is used to predict the target from validation data. The outputs of the independent base learners are then combined to evolve an EML solution.
Unlike the bagging type of the EML method, boosting trains individual learners sequentially on the same data set in an adaptive way. It starts by assigning equal weight to all features. Each subsequent base learner recommends a new weight to the features for the next learner. This is done to create or increase the degree of diversity in the base learners. The outputs of the learners are then combined using the relevant strategy as discussed.
Stacking starts with either bagging or boosting, but the outputs of the learners become input to a meta-model. The meta-model could be—and usually is—another traditional ML algorithm. The meta-model performs the role of an aggregator as it combines the respective outputs of the base learners to evolve the EML result instead of using the averaging or voting methods as previously discussed.
In essence, bagging focuses on getting an EML model with less variance than its base learners while boosting and stacking seek to produce strong models that are less biased than their base learners. A balance between variance and bias is the ultimate goal of the supervised ML methodology.
Random Forest and the General Strategy for Building EML Methods
A typical EML algorithm is the random forest (RF). It is an ensemble of individual decision trees (DT). The DT is a traditional ML algorithm that uses a tree-like model of decisions for deriving a strategy to reach a particular goal. More details on DT can be found in Nisbet et al. (2018).
The fundamental concept behind the RF algorithm is the “wisdom of crowds.” The performance of the RF algorithm is based on the premise that a large number of relatively uncorrelated base learners (individual DTs) operating as a committee will outperform any of the constituent members. It follows the mantra: “the whole is better than the sum of its parts.” This is further strengthened by the diversity among the individual trees. It is based on the assumption that while some trees may be wrong, many others will be right.
The EML method is not limited to RF. It can be built from any traditional ML method using the bootstrapping method or leveraging diverse model parameters. For example, the EML method can be used to overcome the instability of artificial neural networks (ANN) as it is well known to get stuck in the local minimum.
Due to the random initialization of its weights, the results of ANN are not usually consistent. While bootstrapping the data and input features would be a common strategy for all the traditional ML methods, the following are specific possible strategies to create EML algorithms from a few traditional ML algorithms:
- ANN:
- Different number of hidden layers
- Different number of neurons in each hidden layer
- Different learning algorithms (gradient descent, Newton, conjugate gradient, quasi-Newton, Levenberg-Marquardt algorithm, etc.)
- Different activation function (linear, sigmoid, hyperbolic tangent, softmax, rectified linear unit, etc.)
- Support Vector Machines:
- Different kernels (linear, Gaussian, polynomial, radial basis, Laplace, sigmoid, etc.)
- Different values of regularization parameter
- K Nearest Neighbor:
- Different number of “K” neighbors
- Different search methods (Euclidean, city block, Minkowski, Chebychev, exhaustive, etc.)
- Different ways to assign distance weights (equal, inverse, squared inverse, etc.)
- Radial Basis Network:
- Different values of the “spread” parameter
- Different number of neurons
Example Use Cases for EML
Case 1. A typical case that would justify the application of an EML method is when different feature selection algorithms give different results, and domain experts are not fully in agreement with any of them. Different expert petrophysicists may differ on the choice of, and type of, wireline logs to estimate a reservoir’s cementation factor. The cementation factor, the exponent m in Archie’s equation, is a significant input in the estimation of water saturation, which is in turn used for the estimation of hydrocarbon saturation of reservoir rocks. While some may recommend only two (such as gamma ray and resistivity), others may recommend adding density, sonic, and neutron porosity. Others may even prefer to use of all available logs. This diversity can be used as the basis to apply the EML method on this problem. Each expert’s opinion will be implemented in a base learner. Combining the results of all the base learners would evolve a robust overall result. This is illustrated in Fig. 2.
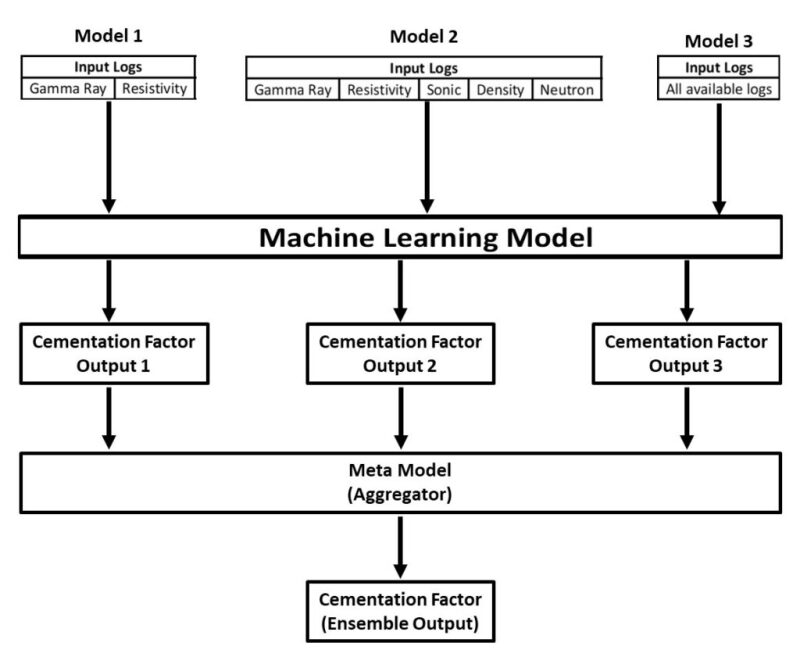
Case 2. Alternatively, we can treat different feature selection algorithms as an expert on the same problem just described. The diversity in the feature importance and ranking results of linear correlation (LC), predictor importance (PredictImp) module of RF or DT, fuzzy ranking (FR), nearest neighbor analysis (NNA), functional networks (FN), etc. can be used as the basis for the EML method. The output of each algorithm can go into a traditional ML method such as ANN. The prediction results based on each feature selection algorithm will be combined using any bagging, boosting, or stacking, to evolve a single overall estimation for the cementation factor. The same Fig. 2 can be used to illustrate this by simply replacing the diverse input logs in Input 1, Input 2, and Input 3 with the diverse features selected by LC, PredictImp, FR, NNA, FN, etc. to become Input 1, Input 2, …, Input n.
Conclusion
Understanding how workflows and methods are designed is key to understanding how they work. This is especially in line with the need to make ML workflows more explainable. Understanding how the ML algorithms work will reduce the black-box phenomenon wrapped around them, and help build more sophisticated algorithms, especially in areas where the traditional ML methods fail to achieve the desired objectives.
Given the theoretical assumptions on which the EML methods are based, there is the need for data science practitioners and enthusiasts to work closely with domain experts. The latter would help to inject a sufficient dose of physical realities to make more sense of the assumptions. It is not just enough to build powerful algorithms. The fundamental principles governing geological, geophysical, and petroleum engineering processes need to be properly considered.
Suggested Further Reading
Anifowose, F.A., Ensemble Machine Learning: The Latest Development in Computational Intelligence for Petroleum Reservoir Characterization, Paper 168111-MS presented at the SPE Saudi Arabia Section Annual Technical Symposium and Exhibition, Dhahran, Saudi Arabia, 19–22 May 2013.
Anifowose, F., Labadin, J., and Abdulraheem, A., Ensemble Machine Learning: An Untapped Modeling Paradigm for Petroleum Reservoir Characterization, Journal of Petroleum Science and Engineering, Volume 151, March 2017, Pages 480–487.
References
Anifowose, F.A., Artificial Intelligence Explained for Non-Computer Scientists, The Way Ahead.
Anifowose, F.A., Hybrid Machine Learning Explained in Nontechnical Terms, Data Science and Digital Engineering.
Dietterich T.G. (2000) Ensemble Methods in Machine Learning. in: Multiple Classifier Systems. MCS 2000. Lecture Notes in Computer Science, vol. 1857. Springer, Berlin, Heidelberg.
Polikar, R., Ensemble Learning, in: C. Zhang and Y. Ma (eds.), Ensemble Machine Learning: Methods and Applications, DOI 10.1007/978-1-4419-9326-7 1, Springer Science+Business Media, LLC 2012.
Nisbet, R., Miner, G., and Yale, K., Classification, in: Handbook of Statistical Analysis and Data Mining Applications, second edition, 169–186, 2018.

Fatai Anifowose is a research scientist at the Geology Technology Division of the Exploration and Petroleum Engineering Center, Advanced Research Center in Saudi Aramco. His career interweaves the artificial intelligence aspect of computer science with the reservoir characterization aspect of petroleum geology. His expertise is in the application of machine learning and advanced data mining in petroleum reservoir characterization. Anifowose has published more than 45 technical papers in conferences and journals. He is a member of SPE; European Association of Geoscientists and Engineers; and Dhahran Geoscience Society, Saudi Arabia. Anifowose obtained his PhD degree from the University of Malaysia, Sarawak, in 2014; MS from King Fahd University of Petroleum and Minerals, Saudi Arabia, in 2009; and BTech from the Federal University of Technology, Akure, Nigeria, in 1999.
[The article was sourced from the author by TWA editors Bita Bayestehparvin, Joon Lee, and Jaspreet Singh.]


