Most petroleum engineers understand that engineering calculations involve the properties of fluids. “Fluid” is a term used to describe gases and liquids. An equation of state (EOS) is nothing more than a fluid model. Specifically, an EOS is a fluid model that takes a molar composition (z) and predicts the phase and volumetric behavior of the fluid (e.g., densities, viscosities and formation volume factors) over a wide range of pressure (p) and temperature (T). However, unlike any arbitrary model, an EOS has certain characteristics that make it particularly useful. Let’s start by looking at those characteristics.
What Makes an EOS an EOS?
An EOS is an equation that relates pressure, volume, temperature and composition (p-V-T-z) of a fluid system. “PVT” is the common term used to describe fluids and their properties in petroleum engineering. An EOS can provide an accurate and reliable PVT model, even for the most complex fluid systems.
Equations of State, What Are They Good For?
The question, “Equations of State, what are they good for?” has probably crossed the minds of many petroleum engineers, both young and old alike. Below are some examples of when an EOS model is particularly useful:
Separation process optimization. In the design process of a new field, it is important to optimize the surface facilities separation processes to maximize oil and liquids production. This is especially important for gas condensate fields, where the separation process can have a significant bottom-line impact on product revenues.
Generating black-oil properties. As a reservoir engineer working on a black-oil reservoir model or a process-engineer working with pipe-flow, have you ever wondered where black-oil properties are coming from? The answer is historically (pre-1980s) from correlations (Standing, Vazquez, etc.), and since the 1980s, usually from an EOS.
Miscibility calculations. If you are working on a gas injection EOR project or a carbon capture and storage project in brown fields, the miscibility design for different fluids is only as accurate as your EOS model.
Estimating reserves. Volatile oil and gas condensate reservoir reserves are strongly dependent on complex fluid properties (condensation and vaporization), and surface separation. Both in-place surface product volumes (and their spatial mapping) and recovery efficiency of products for higher-GOR volatile systems will inevitably depend on accurate EOS modeling.
These are only a few examples, and there are many more.
Well Then, Give Me an Example of an EOS!
Most equations of state used in the petroleum industry are defined using the variable Z
\(Z≡pv/RT\) ........................... (1)
where n is the molar volume defined by the ratio of the volume (V) divided by the molar amount (n) and Z is called the Z-factor.
The simple version of Eq. 1 is Z = 1, the “ideal gas law,” but this is only valid for gases at low pressures and high temperatures where intermolecular forces are negligible.
In the 1940s the Z-factor was accurately (1–3%) correlated graphically for gases by Standing (Standing and Katz, 1944) using reduced temperature and reduced pressure as primary variables. Zg quantified the deviation of gas volumetric behavior from that given by the ideal gas law. Later (1970s), equations were fit to the Standing-Katz Z-factor chart using different forms of the Benedict-Webb-Rubin (BWR) EOS models (e.g., Hall and Yarborough).
By the way, the first EOS published in the petroleum engineering literature was by Starling in 1966 where he applied a BWR EOS to describe both gas and liquid phases. This approach was never embraced in petroleum engineering because of the complexity in solving the BWR EOS. Instead, the cubic EOS was adapted starting in the late 1970s by Katz and coworkers at University of Michigan (e.g., Katz and Firoozabadi, 1978 and Coats, 1980).
What on Earth is a Cubic EOS?
The term cubic relates to the assumption of pressure being expressed as an cubic function of volume. The cubic EOS can be expressed using Z in the general expression
\(A_0+A_1 Z+A_2 Z^2+A_3 Z^3=0\) ...........................(2)
where coefficients A0 to A3 are constants determined by p, T and molar composition (z). These constants are computed from the EOS parameters a and b discussed below.
So, What is a Two-Parameter EOS?
A two-parameter cubic EOS is a PVT equation using two parameters “a” and “b,” as first suggested by van der Waals in 1873, p=RT/(v–b)–a/v2, where a is associated with the attractive force a/v2 between molecules in the fluid and b is associated with the repulsive force RT/(v–b) between molecules in the fluid. Other renowned two-parameter EOS models include Redlich-Kwong, Soave-Redlich-Kwong (SRK), and Peng-Robinson (PR).
So How Do We Use an EOS?
An EOS calculation usually takes a set of fixed (p,T) conditions for a fluid with known composition (zi) and determines whether the fluid is single phase, or splits into two (or more) equilibrium phases. This is called a flash calculation. It requires iteratively solving the material balance Rachford-Rice (or Muskat-McDowell) equation, combined with satisfaction of equal-fugacity (chemical potential) equations for each component. The result of an EOS flash calculation includes phase amounts, phase compositions, and phase Z-factors (densities). EOS flash calculations are required in the reservoir, production tubing, surface facilities, and pipelines, making the flash calculation a main reason why having a good EOS is key to many aspects of petroleum engineering and PVT.
Great, Now What Do These Complicated EOS’ Look Like?
The general equation used for both Soave’s modification of the Redlich-Kwong and the Peng-Robinson EOS is given by
\(p=\) \(RT/(v-b)-a/[v,b]\)........................... (3a)
\(a=Ω_a\) \((R^2 T_c^2)/p_c α(T)\)........................... (3b)
\(b=Ω_b\)\((RT_c)/p_c \)........................... (3c)
\(a ̅=∑^N_{(i=1)}∑^N_{(j=1)}u_i u_j (a_i a_j )^{(1/2)} (1-k_{ij} ) \)........................... (3d)
\(b ̅=∑_{(i=1)}^Nu_i b_i \)........................... (3e)
where ui is a general term for vapor molar fraction (yi), liquid molar fraction (xi), and total mixture (zi).
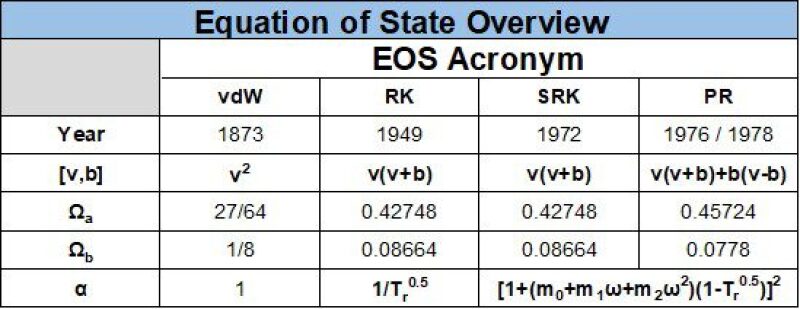
A third parameter c was introduced in 1982 (Peneloux et al.). This third parameter makes a simple volume shift of magnitude c (with molar volume units) for a given phase and a given pressure and temperature—i.e., v = vEOS2–c (e.g., EOS2 = PR or SRK). Often the third parameter is given in dimensionless form, s = c/b. With properly determined values of s (c) for all components, accurate densities of both gas and liquid phases can be expected (±1–3%) at all relevant (p,T) conditions.
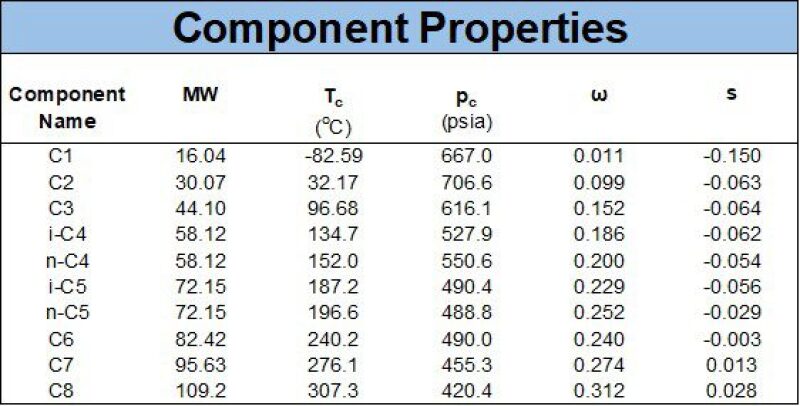
The most common EOS models are the Peng-Robinson (PR) and Soave-Redlich-Kwong (SRK) EOS, which are both two-parameter cubic EOS that have a similar structure. The PR and SRK is always given with two tables, the first table being mandatory and the second table being used in practically all situations. The first table comprises component properties, including critical pressure (pc), temperatures (Tc), acentric factor (ω), molecular weight (M) and volume shift (s or c). An example of the first EOS table is given as Table 2 below.
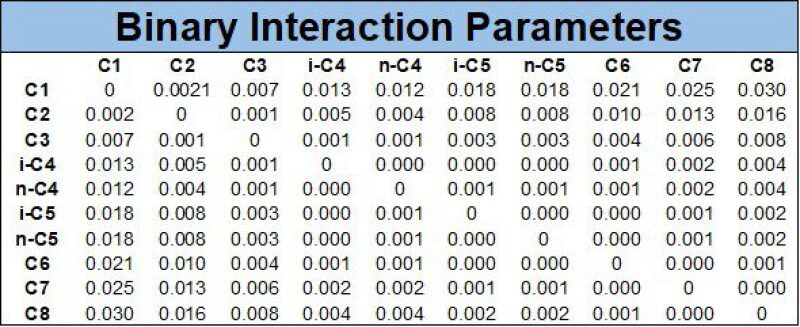
The second table of an EOS defines the binary interaction parameters (kij), which are correction terms applied to each component pair (e.g., C1-C8) in a mixture, with kij=0 being no correction, the magnitude of correction usually being ±0.05–0.2, and symmetry kij = kji.The correction term kij has most impact on the component equilibrium K-values (Ki and Kj, where K = y/x for a given component), particularly at higher pressures.
The example binary interaction parameters (BIP) matrix given in Table 3 uses the common Chueh-Prausnitz (1967) BIP correlation based on component critical volumes vc = RTc/pc.
Rounding Off the Discussion
You will now hopefully have a foundation to understand better what an EOS is, and why they are so useful over a wide range of (p,T) conditions and engineering applications. Hopefully, this will make you a better engineer, student, teacher or boss, and you will be able to see the added value of having a good EOS model for your work as a petroleum engineer.
References
Chueh, P., Prausnitz, J., 1967. Vapor-liquid equilibria at high pressures: Calculationof partial molar volumes in nonpolar liquid mixtures. AIChE Journal, 13, pp.1099–1107.
Coats, K.H., 1980. An equation of state compositional model. SPE Journal, 20(05), pp.363–376.
Hall, K.R., Yarborough, L., 1973. A new equation of state for z-factor calculations. Oil Gas Journal, 71, p.82.
Katz, D., Firoozabadi, A., et al., 1978. Predicting phase behavior of condensate/crude-oil systems using methane interaction coefficients. Journal Pet. Technol., 30, pp.1–649.
Peneloux, A., Rauzy, E., Freze, R., 1982. A consistent correction for Redlich-Kwong-Soave volumes. Fluid Phase Equilibria, 8, pp.7–23.
Peng, D.Y., Robinson, D.B., 1976. A new two-constant equation of state. Industrial & Engineering Chemistry Fundamentals, 15, pp.59–64.
Redlich, O., Kwong, J.N., 1949. On the thermodynamics of solutions. V. An equationof state. Fugacities of gaseous solutions. Chem. Rev. 44, pp.233–244.
Soave, G., 1972. Equilibrium constants from a modified Redlich-Kwong equation of state. Chem Eng Science, 27, 1197–1203.
Standing, M., Katz, D., et al., 1944. Vapor-liquid equilibria of natural gas-crude oilsystems. Trans. AIME, 155, pp.232–245.
Starling, K., et al., 1966. A new approach for determining equation-of-state parameters using phase equilibria data. SPE Journal, 6, pp.363–371.
Markus Hays Nielsen completed his MSc degree at the Norwegian University of Science and Technology in 2020 in the field of reservoir engineering. The topic of his thesis was “The Effect of Binary Interaction Parameters on Phase Behavior.” His advisor was Milan Stanko. During his studies he was a consultant for Whitson on topics ranging from reserve estimations, uncertainty analysis, fluid initialization, fluid modeling, and other PVT-related topics. Nielson is currently a full-time petroleum engineering consultant at Whitson.
[The article was originally published on the Whitson website. Reproduced with permission from the author.]

