The proliferation of high-resolution datasets and decrease in sensor, storage, and computing costs are significantly extending our ability to grasp new concepts, improve predictions, and perform better field decisions. In a matter of a few years, we have also witnessed the consolidation of data science and machine learning as widespread disciplines that could help generate new technologies derived from data. The abundance of data and the persistence of elusive physical laws to satisfactorily explain the complexity of our assets and operations are promoting a renowned interest for finding ways to extend current model capabilities and decision workflow practices. Moreover, the current stringent economic environment and the increasing interest in pursuing cleaner, safer, and cheaper sources of energy are driving the need for more practical but more robust predictive and prescriptive models. Ultimately, the physics we know needs to rely on data to unmask the physics that we do not yet know.
The figure below illustrates how the complexity of our models is forcibly required to decrease as we increase the size of our reservoir models. At the same time, we need to decrease the data resolution due to modeling and computing limitations when looking at larger cases. Ideally, we would like to preserve as much physics and data as possible without compromising speed and flexibility as we tackle increasingly larger reservoir studies.

The oil and gas industry has traditionally relied on empirical and numerical models to explain reality. The advent of data-driven technologies is certainly shaking the basis for this line of thought as many parameters can be simultaneously analyzed to uncover underlying physical laws. Most theoretical methods used in the industry are the result of deriving differential equations that are based on conservation laws, physical principles, and/or phenomenological behaviors for a particular process. These theoretical derivations lead to many of the canonical models of mathematical physics. However, there remain many complex systems that have eluded quantitative analytic descriptions or even characterization of a suitable choice of variables. Take for example the lack of reliable and efficient physical models for describing real-time drilling, wave propagation under the presence of multiple fluids and chemical species on highly fractured media, the changing dynamics of coupled fluid flow and geomechanics in unconventional plays, and the competitive interaction decision and uncertainty parameters for managing the productive life of an oilfield.
Despite the increasing interest in generating business value from data analytics, some practitioners still feel skeptical that a data-driven model can truly overperform or satisfactorily reproduce what current physical models can do. These physics-based models used in the industry are either expressed through a few empirical expressions or sophisticated numerical/visualization tools. Regardless how structurally complex these models are, they are still proxy representations of a preconceived physical reality. In most cases, given its specificity or commercial scope they may be conceptually and computational unsuitable for accommodating additional physical processes.
Whenever robust physics is available, it usually entails computationally intensive processes or workflows. These models may not be suitable for performing real-time actions. The computational demand increases geometrically when these predictive capabilities must be employed to optimize field production operations, well/completion designs, or investment portfolios under uncertainty. To make optimization and uncertainty quantification viable approaches, the physics model must be replaced by data-driven surrogate models that are generated from these physics-based models. The interesting fact is that these data-driven models can be trained using both simulation and field data. The cost of decisions is thus given by the cost of simulation × cost of optimization × cost of evaluating uncertainty scenarios. The goal of a data-driven model is to be able to simultaneously reduce all these multipliers to make the computational cost not just manageable but also amenable for real-time workflows. An example on how to generate a data-driven or reduced physics model (or combination of both) from a high-fidelity physics-based model using optimization can be seen in the figure below.
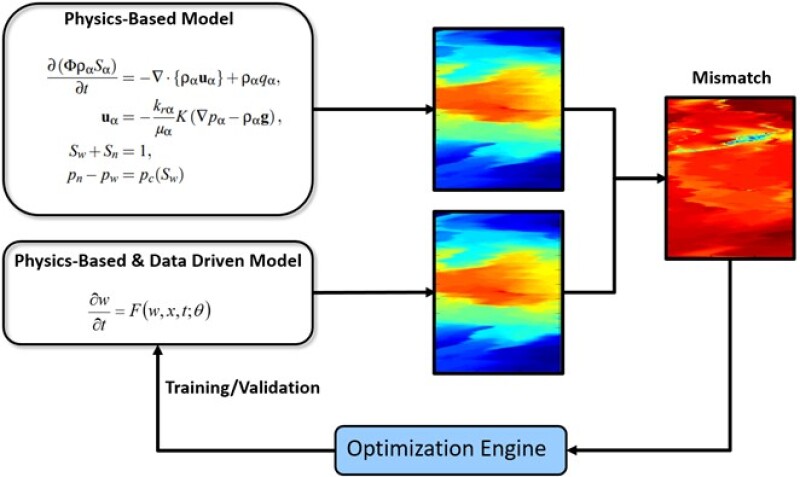
To develop improved predictive models of complex real-world problems, however, one needs to pursue a balanced perspective. Data themselves cannot be an alternative for physical modeling, but when combined with informed and detailed knowledge of the physical problem and its constraints, it is likely to yield successful solutions. The table below summarizes the contrasting perspective between physics-based and data-driven models.
| Lots of Data | Limited Data | |
| Robust Physics-Based Solutions | Hybrid models with improved predictive/prescriptive/cognitive capabilities | Data-driven models designed to emulate physics-based models to increase computational efficiency |
| Lack of Physics-Based Solutions | Data-Driven models suitable to provide insights, predictions, and informed decisions | Need to get more data to gain better insights and understanding about the problem |
As avid engineers interested in streamlining processes it should not come as a surprise to feel naturally inclined to believe that the integration of physics-based and data-driven should look as the most promising path to improve inference, modeling, prediction, and optimization of field operations. The fundamental physics approach would propose the structure of the models, and data analysis would refine possible model structures and determine values or related parameters so robust predictions can be made.
For example, time and spatial dependency are important factors in the resolution of uncertainty associated with oil and gas occurrence and performance. Therefore, hybrid approaches considering both data-driven modeling and physics modeling that considers fundamental analytic relations of time and space seem to be reasonable approaches. The multiple time and space scales we manage in the oil field require further advances in how data are validated and interpreted and, most importantly, how results are communicated fast enough to make the right decisions at the right time.
Production evaluation and reservoir forecasting often demand a significant number of simulations to be able to cope with various field decisions under uncertainty. These challenges become even more daunting when there is a lack of rock/fluid data, insufficient production history, and a limited understanding of the physics governing the flow process. These factors constrain the capability to analyze multiple and possible scenarios and therefore compromise the reliability of field management decisions. In such situations, engineers have relied on a set of analytical models (proxies) for the purpose of predicting flow/production scenarios, monitoring, and performing forecasts that can either alleviate the overwhelming computational burden entailed for existing simulation tools or shed light to improve the physical understanding in the absence of these tools.
Data-driven approaches use information from previously collected data (training data) to identify the characteristics of the currently measured pressure, temperature, or production rate and to predict the future trend. Physics-based approaches assume that a physical model describing the behavior behind these measurements is available and somehow sufficiently accurate and self-contained to predict future behavior. Hybrid approaches combining data with physical assumptions is a valid attempt to connect what we observe with what we can predict and control in the reservoir.
The figure below illustrates that there is a big field of modeling opportunities within the realm of physics-informed data-driven models. This field is suffused with intriguing and unexplored questions. Regardless of the level of physics conceptualization and tools, data-driven mechanisms always represent a valuable opportunity to either increase insights or improve computational performance. Are we ready to tackle these challenges?
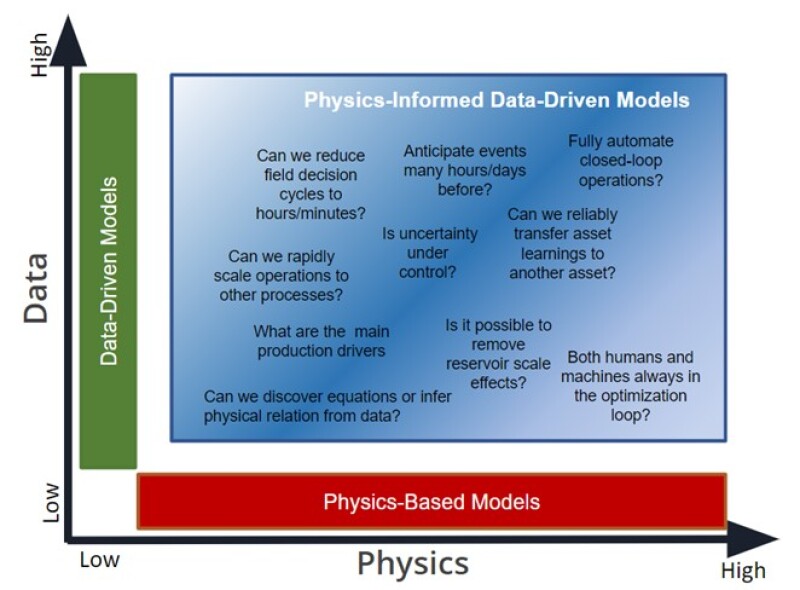
One intriguing question that has been troubling engineers for many years, is to know how accurate and fine a model needs to be solved to achieve a reliable decision under the underlying reservoir uncertainty. Although this question may be impossible to answer thoroughly, its quest certainly triggers alternative ways to automate our field operations. Hence, is it possible to surpass the predictive power of current simulations through a new class of models that are driven by data and obey physical principles?
References
Karpatne, A., Atluri, G., Faghmous, J.H., et al. 2017. “Data Science: A New Paradigm for Scientific Discovery from Data.” IEEE Transactions on Knowledge and Data Engineering, 29 (10), 2318–2331.
Klie, H., 2015. “Physics-based and Data-Driven Surrogates for Production Forecasting.” SPE Reservoir Simulation Symposium. SPE-173206-MS, SPE Reservoir Simulation Symposium, February 23–25.
Klie, H. and Florez, H. 2020. Data-Driven Prediction of Unconventional Shale-Reservoir Dynamics. SPEJ, 25 (05): 2564–2581.
Klie, H., Klie, A., and Bicheng, Y. 2020. “Data Connectivity Inference and Physics-AI Models for Field Optimization.” URTEC-2020-1098-MS. SPE/AAPG/SEG Latin America Unconventional Resources Technology Conference. Virtual November 2020.
Willard, J., Jia, X., Xu, S., et al. 2020. Integrating Physics-Based Modeling with Machine Learning: A Survey. Submitted to ACM Computing Surveys.
Willcox, K., Ghattas, O., and Heimbach, P., 2021. “The Imperative of Physics-based Modeling and Inverse Theory in Computational Science.” Nature Computational Science, March, pp. 166–168.


