This article explores how scalable modeling and simulation methods, incorporating physical, operational, and geometric constraints, can improve the practical design of subsurface CO2 storage systems. Through constrained optimization workflows, the approach enables decisions that align technical feasibility, regulatory compliance, and long-term storage performance.
The New Frontier of Subsurface CO₂ Storage
Geological CO2 storage is central to industrial decarbonization efforts. As projects move from conceptualization to implementation, the focus shifts from identifying storage sites to designing them for safe, scalable, and sustained injection performance. Achieving this requires not just pore space, but intelligent system design, especially in how wells are placed and operated.
Real-world CO2 storage projects are shaped by subsurface heterogeneity, nonlinear flow dynamics, and complex pressure interactions across space and time. Static models and single-scenario simulations are insufficient to navigate these complexities. What’s needed are modeling and simulation workflows built around constrained optimization frameworks that incorporate physical feasibility and enable scalable, adaptive design from the outset. This evolution marks a shift from modeling what is theoretically possible to engineering solutions that are robust, practical, and aligned with the demands of field-scale deployment.
From Bound-Constrained Optimization to Realistic Storage Design With Nonlinear Constraints
A critical decision in subsurface CO2 storage system design is where to place the wells. Well placement directly influences injectivity, pressure buildup, plume migration, and overall storage efficiency and integrity. Optimizing this placement is inherently complex, as it must account for geological heterogeneity, flow dynamics, and operational constraints, requiring methods that balance physical feasibility with performance-driven objectives.
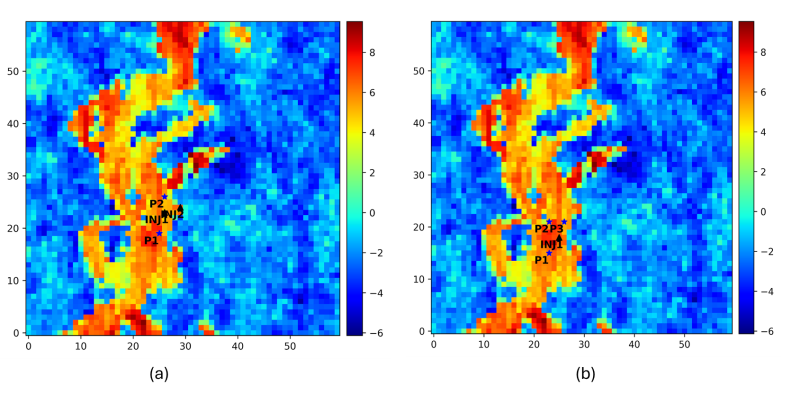
In my work published in SPE Journal, I investigated this challenge by applying gradient-free optimization methods to maximize net present environmental value (NPEV) in a simplified subsurface CO2 storage setting under bound constraints. The optimization problem involved selecting the spatial locations of CO2 injectors and brine producers within a channelized heterogeneous reservoir, constrained only by upper and lower coordinate bounds for each well. While the methods demonstrated good convergence, the resulting well configurations consistently placed brine producers close to injectors (Fig. 1). Although this setup yielded high economic returns, it led to significant CO2 production, undermining long-term containment goals and operational feasibility.
These results underscored a critical insight: bound-constrained optimization may produce technically optimal outcomes, but without accounting for realistic system constraints, it can yield solutions that are physically impractical or environmentally unsound.
In a subsequent study, I developed an optimization framework that explicitly incorporates nonlinear constraints into the well placement and control design process, addressing the limitations of bound-constrained optimization and better reflecting field-relevant operational challenges. This framework integrates the iterative Latin hypercube sampling technique (ILHS) with two constraint-handling strategies: the Augmented Lagrangian Method (ALM) and a Filter Method. This framework is fully compatible with black-box reservoir simulators and does not require gradient information, making it especially suitable for complex, field-scale models where analytical derivatives are unavailable.
By directly embedding constraints into the optimization logic rather than treating them as post-processing checks, the framework enables more realistic and operationally feasible designs for CO2 storage systems.
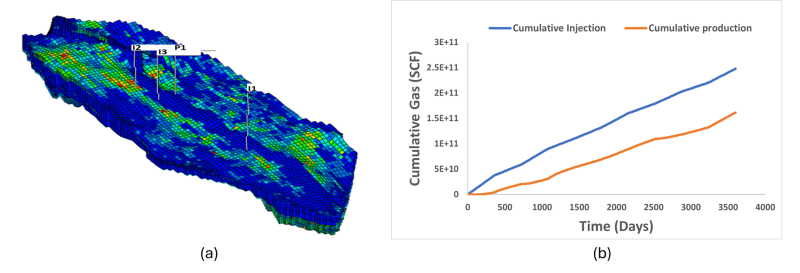
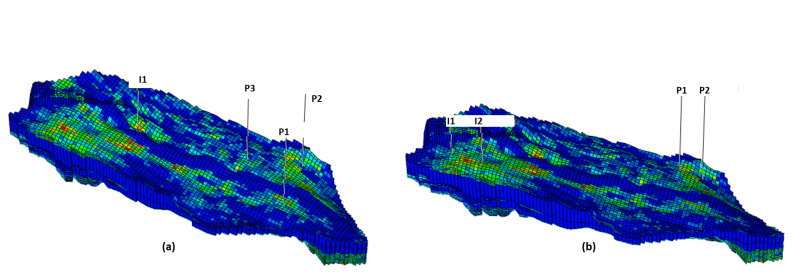
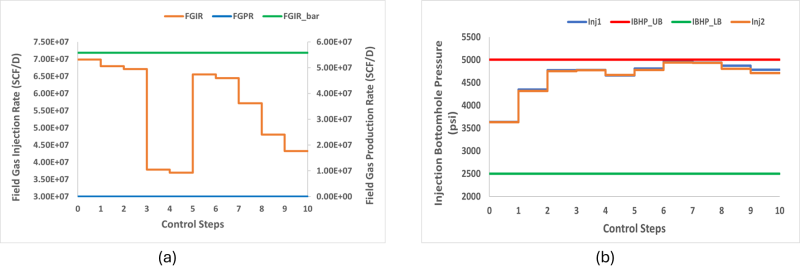
To demonstrate the practical relevance and effectiveness of the proposed optimization framework, I applied it to three CO2 storage optimization case studies, each incorporating additional nonlinear constraints to reflect increasing levels of operational realism. In the first scenario, the optimization problem involved selecting the well locations and control strategies for three injectors and one producer, while enforcing a nonlinear constraint on the injection bottomhole pressure (IBHP) (Fig 2).
Although the optimization successfully identified feasible solutions that honored the IBHP constraint, the resulting well configurations placed the producer very close to the injectors. This proximity led to excessive CO2 co-production, amounting to nearly 65% of the injected CO2 being produced, revealing a key shortcoming of the problem formulation. The lack of an explicit constraint on CO2 production allowed economically favorable but physically undesirable outcomes. This insight motivated the inclusion of a field gas production rate (FGPR) constraint in the second scenario.
The second scenario increased the design complexity by allowing the optimization to choose well types, in addition to their locations and controls (Fig 3). A strict FGPR constraint was introduced to limit CO2 production to no more than 5% of the total injected volume. While this constraint was fully satisfied, effectively minimizing gas production and maintaining containment, it restricted the inclusion of producers in the system.
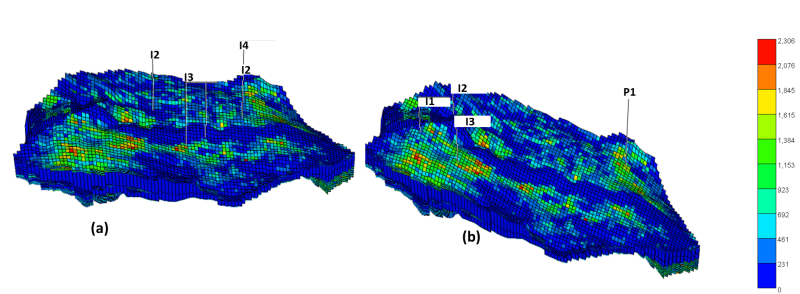
As a result, the reservoir lacked sufficient pressure relief, which led to consistent violations of the IBHP constraint, particularly under sustained injection (Fig. 4). The optimization favored solutions with primarily injector wells, which reduced CO2 production but also limited operational flexibility and lowered the achievable NPEV, demonstrating the tradeoffs imposed by overly strict or conflicting constraints.
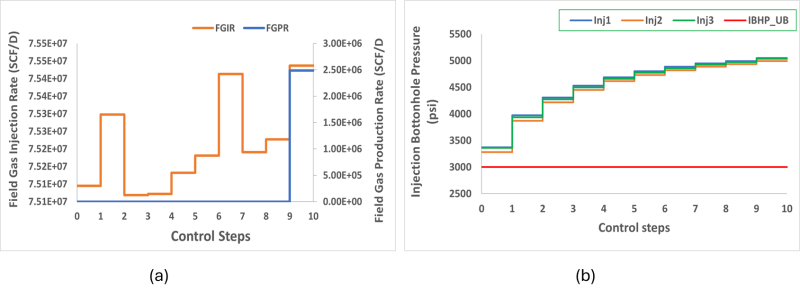
To improve feasibility and better reflect real-world operating conditions, the third scenario relaxed the constraint parameters by raising the IBHP upper limit to 5,000 psi and loosening the FGPR constraint to 20% of the total injection. These more realistic bounds expanded the feasible solution space and enabled the identification of more balanced well configurations (Fig. 5). The optimization was able to converge toward feasible designs with mixed well types and better alignment between injectivity, pressure management, and containment.
Across all three cases, the results underscored the importance of thoughtful constraint formulation. Constraints that are too lenient can permit counterproductive outcomes, while overly strict constraints can eliminate viable solutions and hinder optimization progress. Properly tuned constraints, on the other hand, enable robust, field-ready subsurface storage designs.
Geometric Constraints and Reservoir-Specific Feasibility
Beyond operational and policy-related constraints, subsurface CO2 storage design must also satisfy geometric feasibility—ensuring that wells are placed within accessible, safe, and technically viable regions of the reservoir. Traditional methods for geometric constraint handling, such as penalty functions or sample repair procedures, often rely on adjusting infeasible solutions after generation. However, these approaches can be inefficient, may not guarantee feasibility, and can interfere with the sampling logic of scalable algorithms like Iterative Latin hypercube sampling (ILHS).
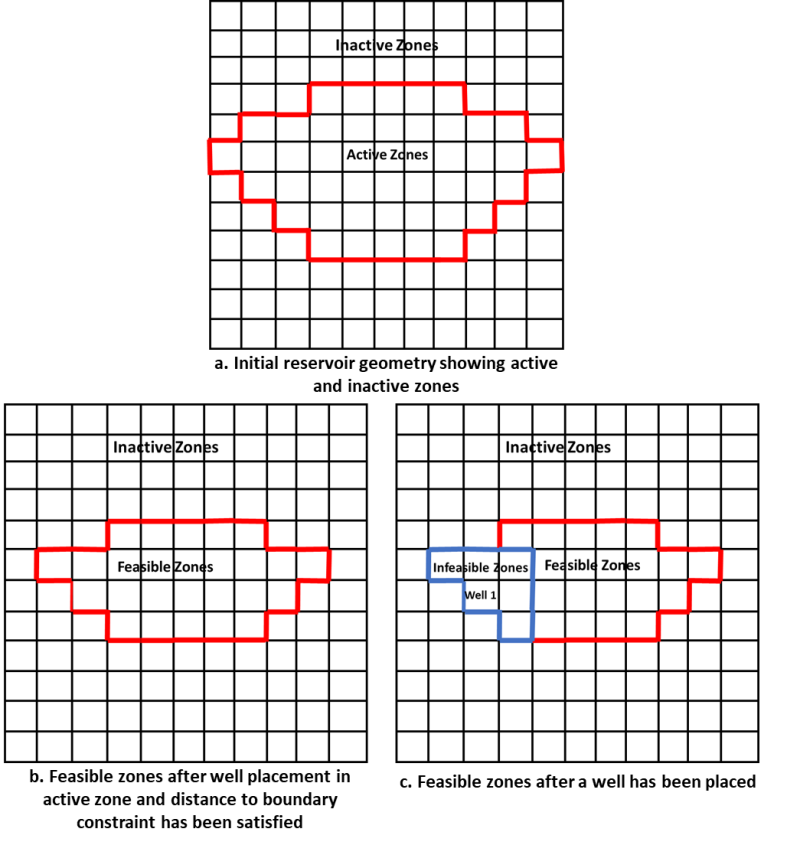
To overcome these limitations, I developed a novel geometric constraint-handling method tailored to grid-based reservoir models (Fig. 7). This method avoids post hoc repairs by dynamically constraining the search space during the sampling process. Specifically, it defines geometric feasibility based on three core criteria: (1) all wells must be located within active grid blocks of the reservoir, (2) each well must maintain a minimum distance from the reservoir boundaries, and (3) wells must satisfy a minimum interwell spacing requirement.
The algorithm works by first generating a Boolean mask of the reservoir's top layer, marking inactive or geometrically restricted grid blocks as infeasible. When placing wells, the method transforms scaled sample coordinates into physical grid indices and maps each well into an active zone that satisfies the minimum boundary distance. After each well is placed, the mask is updated to mark nearby grid blocks as temporarily inactive, preventing subsequent wells from violating the interwell spacing rule. This iterative update ensures that all wells in a given sample are both spatially and operationally viable before simulation.
This approach is especially effective in large, heterogeneous reservoirs where spatial limitations—such as surface access, infrastructure layout, or fault zones—must be respected. By embedding geometric constraints into the core sampling logic, the method maintains the integrity of the ILHS algorithm while eliminating the need for corrective adjustments. It ensures that every sample generated is not only simulation-ready but also field-deployable, making it well-suited for full-field development scenarios where physical deployment constraints are non-negotiable.
Key Takeaways and Broader Applications in Subsurface Engineering
As the energy industry pursues large-scale decarbonization, the challenge is no longer limited to identifying suitable geological formations for CO2 storage, it is designing them for reliable, regulated, and long-term operation. This article demonstrates that constrained optimization, when embedded in simulation workflows and informed by both nonlinear and geometric feasibility logic, provides a viable pathway to achieve that goal. Rather than treating physical constraints as afterthoughts, the framework integrates them into the optimization logic from the outset—yielding solutions that reflect the operational, spatial, and policy realities of field-scale deployment.
The results showed that optimization outcomes shift dramatically when real-world constraints such as pressure limits and CO2 production thresholds are imposed. Without properly defined nonlinear constraints, well placements favored boundary zones and clustering between injectors and producers to maximize short-term injectivity and economic return. However, these configurations risked excessive plume migration and CO2 breakthrough. When the constraints were integrated, the optimal solutions changed substantially: injectors moved toward geologically central locations to manage pressure buildup, and producers were spaced farther from injectors to satisfy FGPR constraints and minimize co-production of CO2. These shifts weren’t minor adjustments, as they redefined what it means for a design to be optimal under regulated, operational conditions.
The constrained optimization framework presented here extends beyond the configuration of CO2 storage systems to support wider applications across the subsurface engineering domain. The foundational elements of this workflow, including nonlinear constraint handling, geometric feasibility logic, and scalable, gradient-free optimization are applicable to a wide range of subsurface design problems. Whether in hydrogen storage, natural gas storage, geothermal wellfield development, or critical mineral recovery, the need to design systems that balance spatial feasibility, operational performance, and regulatory compliance is universal. By embedding these considerations directly into the modeling and optimization process, this approach empowers engineers to produce development plans that are not only technically sound, but operationally viable.
For Further Reading
History Matching With Iterative Latin Hypercube Samplings and Parameterization of Reservoir Heterogeneity by T. Goda, K. Sato, The University of Tokyo.
A Derivative-Free Methodology With Local and Global Search for the Constrained Joint Optimization of Well Locations and Controls by O. Isebor, L. Durlofsky, Stanford University; D. Echeverría Ciaurri, IBM.
Performance Comparison of Gradient-Free Optimization Methods for Well Placement and Well Controls Optimization for Geologic CO2 Storage by I. Tom, Q. Nguyen, M. Onur, University of Tulsa
Nonlinearly Constrained Well Placement Optimization for Geologic CO2 Storage Using Iterative Latin Hypercube Sampling by M. Onur, I. Tom, University of Tulsa, Q. Nguyen, ExxonMobil
Effective Treatment of Geometric Constraints in Derivative-Free Well Placement Optimization by A. Zou, T. Ye, O. Volkev, Stanford University, et al.

