This article provides an overview of two novel applications of the capacitance model, including its implementation during the primary production period and in gas reservoirs.
The Capacitance Model (CM), also called the Capacitance Resistance Model (CRM), is a data-driven method that has been successfully applied mostly in waterflooding projects. CM was developed by coupling the material balance equation with a linear productivity model (Yousef et al. 2006) using superposition in space. This type of coupling was originally developed for a combination of capacitors and resistors in a circuit system in electrical engineering. The final equation of this coupling method gives the production rate for each producer as a function of the injection rates of the surrounding injectors and the producers’ bottomhole pressure (BHP) in a system, which includes j producers and i injectors (Eq. 1).
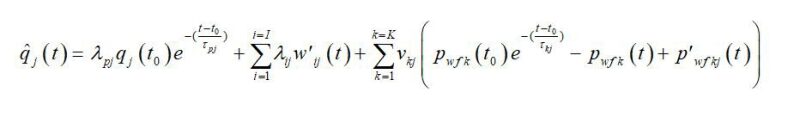
where
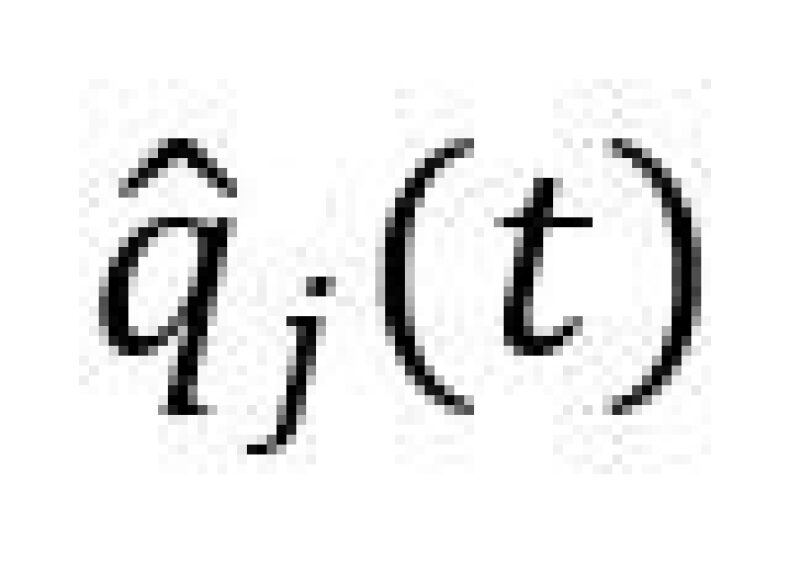
is the estimated total production rate of producer j,
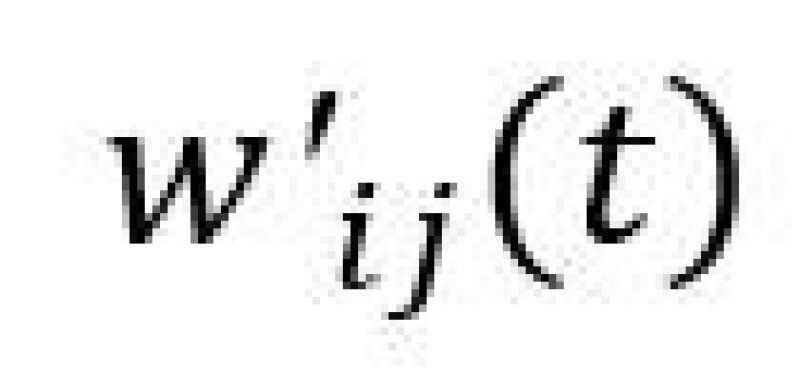
are the shifted injection rates,
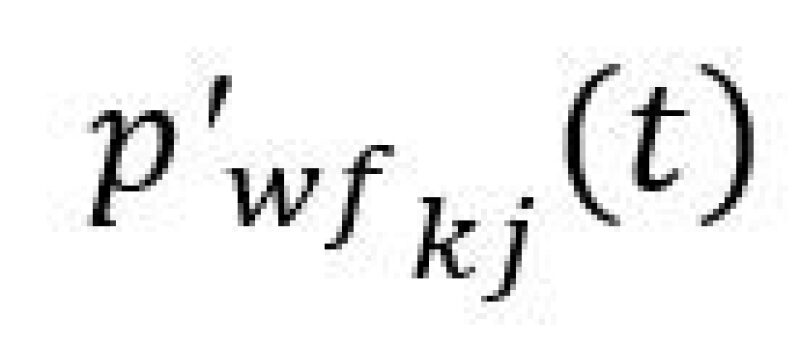
are the BHP values (Yousef et al. 2006, Kaviani et al. 2012), λ’s are regression weight factors which quantify the degree of connectivity (communication) between injector-producer pairs, \(\tau\)s are time-constant parameters which quantify the degree of storage or time lag between well pairs, and \(\nu\)s are weight factors for the effects of producer BHPs on the producer’s rates. The values of λ, \(\tau\), and \(\nu\) are constants, determined by non-linear regression. The right side of Eq. 1 can be simplified to the summation of a primary production term (first term), a waterflooding term (second term), and a BHP term (third term).
The two objectives of CM are to estimate production rate and evaluate inter-well connectivity using the connectivity parameters (λs). Using enough data points (historical production, injection, and BHP data) as inputs and utilizing a non-linear regression model, all constants are estimated and the model is trained for the prediction period. To implement this model for field applications, several modifications have been made. (Sayarpour et al. 2009, Kaviani et al. 2012, Soroush et al. 2013, 2014). Although most applications of CM are in waterflooding projects (Soroush et al. 2014, Kaviani et al. 2014, Soroush et al. 2018, Soroush 2014), CM has also been implemented in immiscible gas injection processes (Yousef et al. 2019).
Fig. 1 illustrates CM application for a simple waterflooding case study. No communication is assumed between injector 1 and producer 2. Therefore, the waterflooding term in Eq. 1 can be omitted as λ between these two wells approaches zero. On the other hand, there is a good communication between injector 1 and producer 1, thus all terms in Eq. 1should be considered.
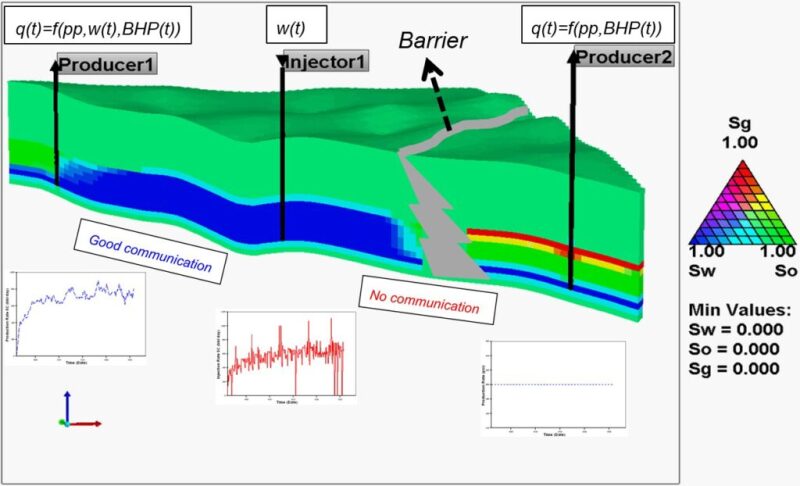
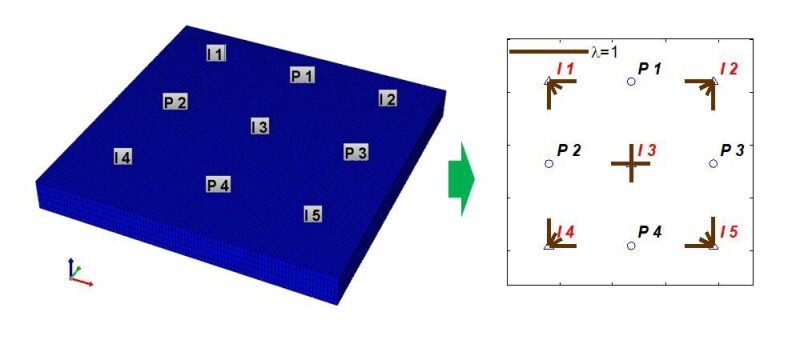
Fig. 2 demonstrates a visual description of the connectivity parameters (λ) for a homogenous system composed of four producers and five injectors. Each line represents a λ value between an injector/producer pair, with its length being proportional to the magnitude of l, which ranges from zero to one. A longer distance between the two wells means lower communication and a smaller λ. CMG-IMEX was used to generate a synthetic model of a typical conventional oil reservoir and to extract monthly production-injection data for 10 years (Soroush 2014). For heterogeneous systems, λ changes according to the degree of communication and the distance between the wells. In summary, CM implementation involves: collecting production-injection data taken from the field or from simulations; using Eq. 1 and a non-linear regression algorithm through which production-injection data are used as inputs or training data to obtain constant parameters (λ, \(\tau\) and \(\nu\)); and mapping constant parameters (mainly λ) to evaluate inter-well connectivity; and using these parameters in Eq. 1 to estimate production rate.
Application of CM During the Primary Production Period in Oil Reservoirs
Two approaches were proposed for the application of CM during the primary production period in oil reservoirs (Soroush and Rasaei 2018).
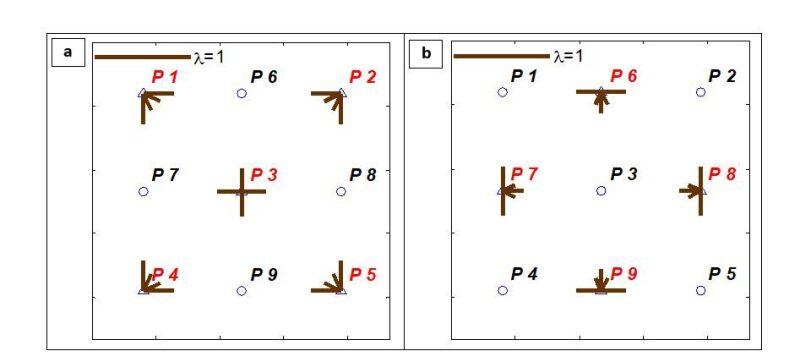
The first approach involves a pseudo-injectors method, which assumes that some of the producer wells are pseudo injectors with negative rates. A new term is introduced to the CM equation to include the aquifer contribution (Eq. 2). The weight factors \(\alpha\) indicate the aquifer strength for a specific producer. Fig. 3 shows a line plot for the connectivity parameters (λ) using the pseudo-injectors approach for a homogenous reservoir with nine producers (Soroush and Rasaei 2018).
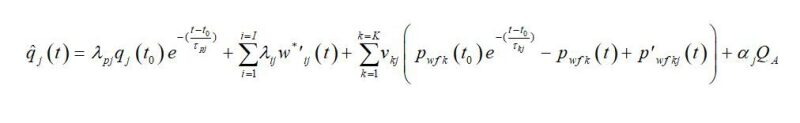
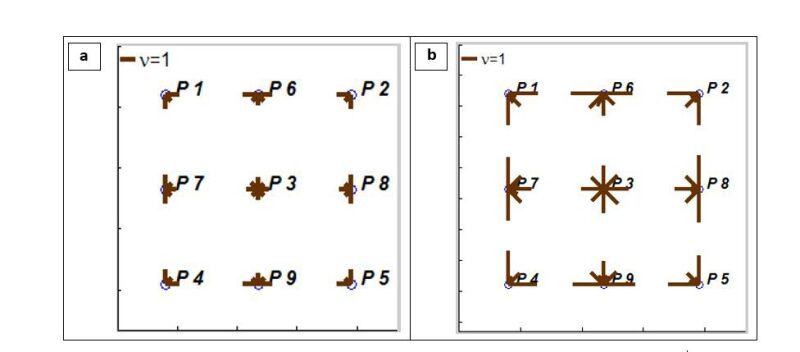
The second approach involves a BHP method, where the matrix form of the productivity model is coupled with the material balance equation. The CM final equation adopts a matrix form in which production rates are given in terms of the producers’ BHPs (Eq. 3). Fig. 4 shows a line plot for connectivity parameters (\(\nu\)) using the BHP method for a homogenous reservoir with nine producers at 100 mD and 200 mD permeability. In Eq. 3, production rates and BHP values are given in vector form while weight factors are given in matrix form. The connectivity values are positively correlated to permeability (Fig. 4); average or local permeability values can be estimated using the BHP method.
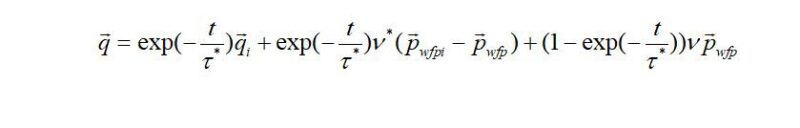
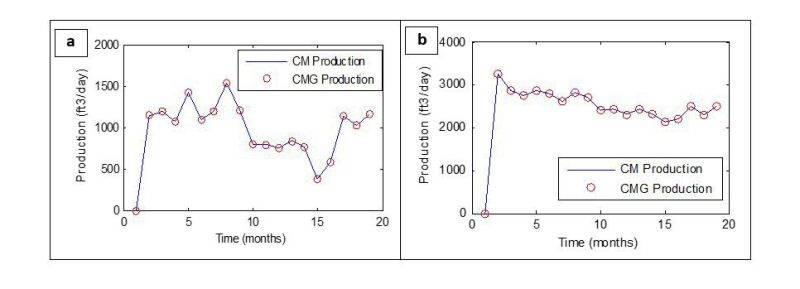
Moreover, the BHP method can be used to predict production rate of each producer well. Fig. 5 presents a comparison between the estimated production rate using CM and CMG simulation results.
Application of CM in Gas Reservoirs
Using CM in gas reservoirs can be challenging because various fluid properties (density, compressibility factor, viscosity, and formation volume factor) change with pressure. The linear productivity model, which was used in the CM equation derivation, is valid only for small reservoir pressure changes in gas reservoirs. For some deep gas reservoirs, this assumption is applicable and makes Eqs. 1–3 valid.
Nevertheless, the CM equations should be modified for gas reservoirs when the pressure change is significant. This modification includes the use of a pseudo-pressure equation instead of pressure in the productivity model. Fluid properties in the CM equation vary with pressure and should be updated at each time step.
Advantages of CM Against Other Methods
CM is a data-driven fast and easy tool, based only on production rate and BHP data. The main advantage of CM is that it is cost-effective and does not need field or laboratory testing such as geological and PVT data that are necessary for conventional simulation models. At the same time, CM is unlike a statistical proxy model which requires a large number of data to be fine tuned. Kaviani et al. (2014) present a procedure for determining the number of data points, which would suffice for reliable CM application.
Benefits of CM Application During the Primary Production Period
CM can potentially become a more efficient tool if it is applied a priori to IOR projects to determine the optimal IOR strategy for a particular field. For instance, in a highly heterogeneous reservoir with faults present, utilization of CM can better guide operators in IOR well pattern determination based on the estimated connectivity parameters.
References
Kaviani, D., Jensen, J.L., and Lake, L.W. 2012. Estimation of Interwell Connectivity in the Case of Unmeasured Fluctuating Bottomhole Pressures. Journal of Petroleum Science and Engineering, 90-91 (1): 79-95.
Kaviani, D., Soroush, M., Jensen, J. L. 2014. How accurate are Capacitance Model connectivity estimates? Journal of Petroleum Science and Engineering Volume 122, Pages 439–452.
Sayarpour, M. 2008. Development and Application of Capacitance/Resistive Models to Water/CO2 Floods. PhD dissertation, The University of Texas at Austin, Texas.
Soroush, M. 2014. Interwell Connectivity Evaluation Using Injection and Production Fluctuation. PhD dissertation, The University of Calgary.
Soroush, M. and Rasaei, M. R. 2018. Application of the Capacitance Model in Primary Production Period before IOR Implementation. Society of Petroleum Engineers. SPE 191236-MS.
Soroush, M.; Jensen, J.L.; and Kaviani, D. 2013. Interwell Connectivity Evaluation in Cases of Frequent Production Interruptions. SPE 165567.
Soroush, M.; Kaviani, D.; and Jensen, J.L. 2014. Interwell Connectivity Evaluation in Cases of Changing Skin and Frequent Production Interruptions. Journal of Petroleum Science and Engineering, Volume 122, Pages 616–630.
Yousef, A.A.; Gentil, P.; Jensen, J.L. et al. 2006. A Capacitance Model to Infer Interwell Connectivity From Production and Injection Rate Fluctuations. SPEREE 9(5): 630-646.

Mohammad Soroush is a research engineer at RGL Reservoir Management with a focus on machine learning and signal processing. He earned his BSc and MSc degrees in petroleum engineering from the Petroleum University of Technology in Iran and MEng and PhD degrees in petroleum engineering from the University of Calgary. He worked at the Tight Oil Consortium (a consulting team of reservoir characterization and engineering experts at the University of Calgary) as a postdoctoral scholar and at the University of Trinidad and Tobago as an assistant professor. Soroush has more than 10 years of teaching/research and professional experience in petroleum engineering and reservoir characterization.
The main area of Soroush’s research are reservoir engineering and production optimization, analytical and numerical (simulation) modeling, integrated reservoir characterization, geostatistics, machine learning, data analytics, and enhanced oil recovery of conventional, heavy oil, and tight/shale gas reservoirs. Currently, he is developing a framework to use the data from fiber-sensing technologies to smart-monitor oil and gas reservoirs. More specifically, he is working on signal processing methods and machine learning algorithms to analyze and understand the fiber-sensed signals.
[The article was sourced from the author by TWA Editor Ali Habibi.]