Individuals who have dedicated their careers to the advancement and improvement of the oil and gas industry and have made significant contributions to it are considered Pillars of the Industry and are featured in this section.
In this issue, Abbas Firoozabadi of the Reservoir Engineering Research Institute and Yale University and Hussein Hoteit of ConocoPhillips engage in an interesting review of traditional (“old school”) numerical-simulation approaches and explain the need to change (to “new school”) reservoir-simulation approaches. They seek to spark interest among young professionals and the industry at large in embracing a new line of attack for complex reservoir-simulation problems.
In a second article, Ganesh Thakur of Chevron explains how technical professionals in our industry are being challenged to develop and apply innovative (“new school”) solutions to emerging, complex, and multifaceted problems that typically require much more than the sometimes outdated (“old school”) industry-standard practices. Thakur emphasizes the strategic importance of technical professionals to our industry and elaborates on what is required from industry to retain this much-needed talent.
It is our intention that TWA readers can find in these pillars of our industry a source of inspiration that can shape their own industry contributions. We thank our authors for their lifetime contributions and hope that you benefit from their articles—Luis F. Ayala, Editor, Pillars of the Industry
We began a major research effort on production and recovery mechanisms in fractured petroleum reservoirs in 1990. By 1998, the research efforts gave us a clear understanding of various processes including reinfiltration and the effect of capillary pressure contrast. During the same period, we also made efforts to simulate laboratory flow testing. The senior author was also involved in the study of several fractured reservoirs in different parts of the world. It was gradually recognized that the available numerical-simulation models were not fit for the study of some of the fractured reservoirs, nor can they be used for some laboratory-scale problems. After an extensive literature review in various disciplines, we embarked on reservoir simulation research with the intention of developing new models for simulation of fractured reservoirs. We were convinced that a new approach is needed. In this article, after a brief review of the three approaches in reservoir simulation, results of our recent efforts in the simulation of complex reservoir problems are presented.
Classification of Reservoir Simulators
There are three broad classes of numerical approaches in reservoir simulation. The predominant method is based on the finite-difference (FD) method. In this approach, the Taylor-series expansion is used to define the derivative functions in governing flow equations. Most commercial models use the first order form of the approximation of derivatives. As a result, state variables such as saturation and composition are computed to be constant in a computational grid cell. Pressure is calculated at a fixed point such as the grid-cell center or as an average cell pressure. There are a few inherent advantages of the FD method including (1) simplicity, (2) ease of extension from 1D to 2D and 3D, and (3) compatibility with certain aspects of physics of two- and three-phase flow. Disadvantages include (1) numerical dispersion, (2) grid dependency, and (3) inaccuracy in flux calculations in heterogeneous media with capillary pressure contrast. Another inherent limitation of the FD method is that it is difficult to adapt for unstructured gridding in a simple way, especially in 3D. The use of the FD method for nonorthogonal corner-point-geometry grids may introduce significant errors.
A second method is the finite-volume (FV) approach, which can be described as an FD method applied to the integrated form of the governing flow equations. The integrated form allows for unstructured gridding. Issues of numerical dispersion, grid orientation, and, to a lesser extent, flux calculation can still be serious for complex problems such as fractured reservoirs.
The finite-element (FE) method is an alternative approach. It has some powerful features, provided attention is paid to the physics of multiphase flow in porous media. In this method, the unknown variables, such as saturation or concentration, are approximated by using known test functions, which can be linear or higher-order polynomial expansions in terms of unknown variables at the geometric locations (nodes) when the FE (or grid-cell) shapes are defined. As a result, variables such as saturation can vary within a given cell or element, which results in low numerical dispersion. The FE method is also flexible for unstructured gridding.
Drawbacks of the FE method, or the FD and FV methods with higher-order approximations, include unphysical oscillations that require post-processing after each timestep, by methods such as the slope limiters. Another drawback, as mentioned above, may relate to the need for close attention to the physics of multiphase flow. For example, if one uses the continuous Galerkin method, a problem may arise because one does not allow for discontinuous saturation at the nodes. As a result, the continuous Galerkin method does not fit the two-phase flow in heterogeneous media with capillary heterogeneity. The discontinuous Galerkin (DG) method, on the other hand, removes the deficiency and provides an accurate solution because it also allows for sharp changes in saturation.
The computation of the flux at the interface between grid cells in two-phase flow with capillary pressure heterogeneity can be a major source of inaccuracy. Let us consider a simple 1D domain with permeability heterogeneity in which pressure data at the grid-cell centers is available. In single-phase flow, one can use a geometric permeability mean and calculate the flux between the two cell centers at the interface. In two-phase flow with capillarity, such a method may not be accurate. In other words, when all the pressures (or potentials) at the cell centers are available, one does not know the pressure or potential gradients at the interfaces to calculate the flux. When the pressure (or potential) at the interfaces is available, then the flux can be calculated readily. The mixed-finite-element (MFE) method overcomes the difficulties of flux calculation in heterogeneous media in two-phase flow. In this method, one calculates the cell average pressure (or potential) and the interface average pressure (or potential) in the FE framework. As a result, there is no need for special treatments in applications to fractured media and complex domains with barriers. It also allows inclusion of permeability anisotropy of very high degrees.
Reservoir Simulation of Complex Problems
Complex reservoir problems demand careful reservoir-simulation studies. The complexity results either from reservoir characterization (e.g., heterogeneity and anisotropy in permeability) or from the process for oil recovery (e.g. capillarity, gravity, and phase behavior), or from the combination. Dual-porosity modeling has been used in the industry to simulate fractured reservoirs. The model has a sound basis in single-phase flow. It also may be useful in water injection for water-wet reservoirs where fractures are uniform and orthogonal. Despite many useful features, the dual-porosity model cannot provide reliable results in the simulation of gas-injection processes or of reservoirs in which fractures do not intersect. It also does not describe discrete fractures.
The combination of the MFE and DG methods and the use of certain physical concepts may provide a powerful alternative in simulating fractured reservoirs, as well as heterogeneous reservoirs. Inherent features of the MFE method allow major advances in simulation of complex problems, provided the implementations are based on physics. Here we present three examples to demonstrate powerful features from the use of advanced concepts.
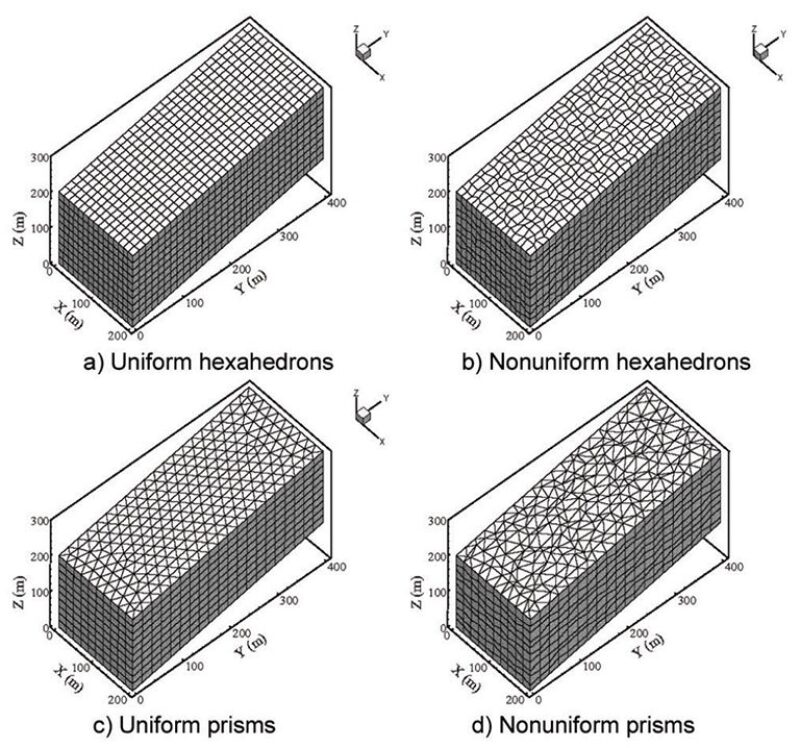
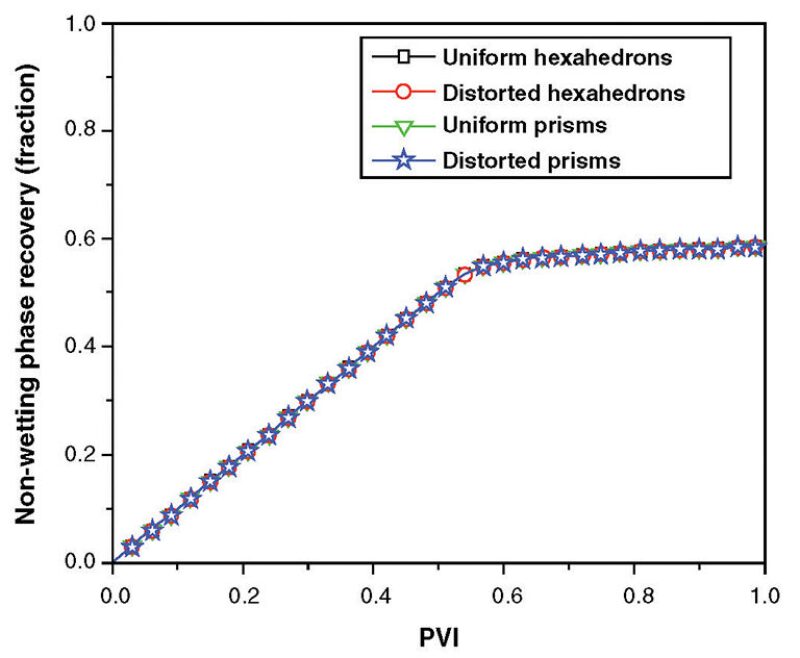
Grid Dependency. Use of first-order methods may result in significant grid orientation effects. Fig. 1 shows various mesh elements used for a 3D tilted reservoir. In this example, water is injected at one bottom corner, and oil and water (after breakthrough) are produced from the opposite top corner. Cumulative oil production is shown in Fig. 2. The use of the combined MFE and DG methods provides reliable results with very little grid dependency, even for nonorthogonal grids of low quality.
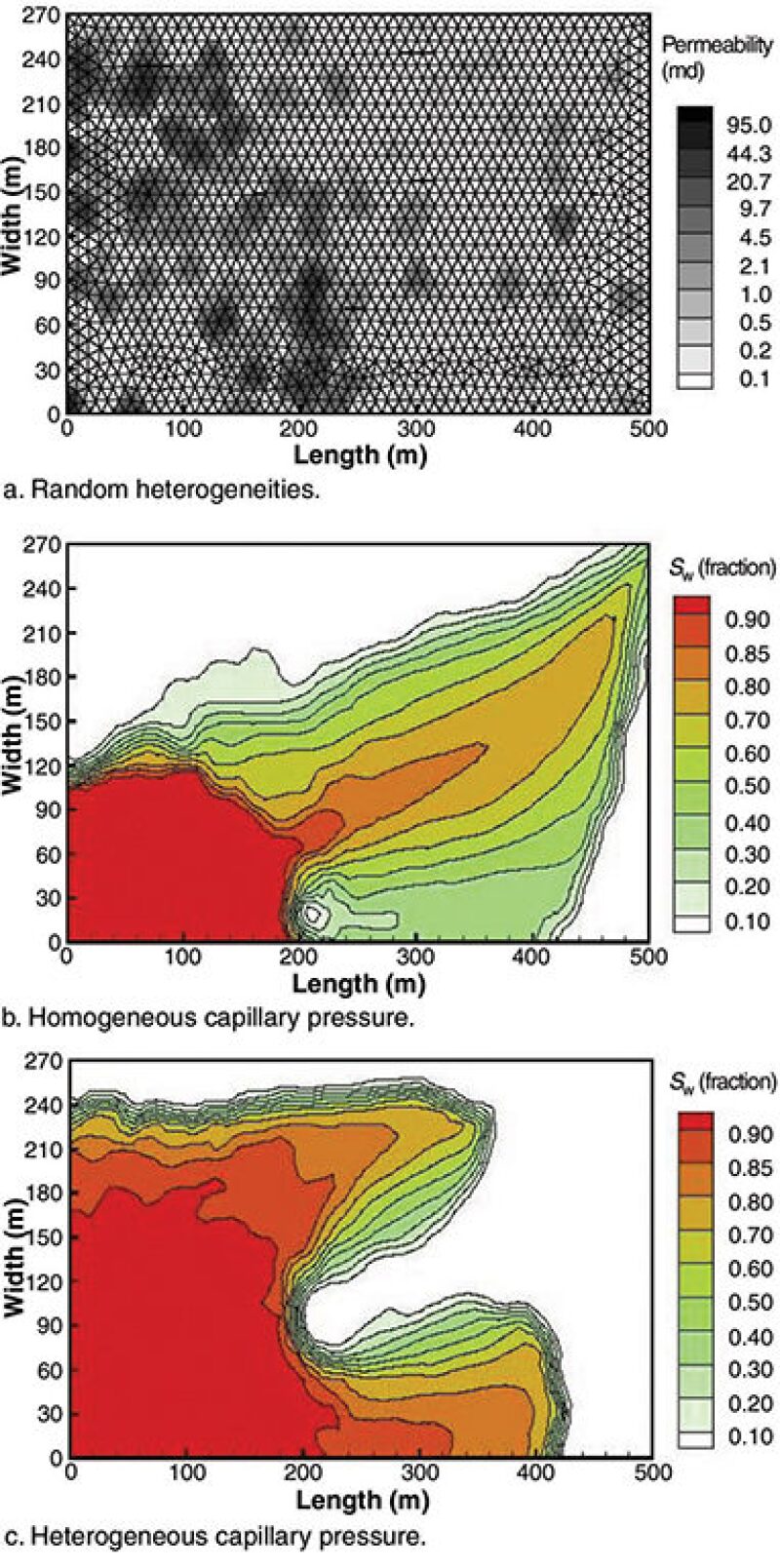
Heterogeneous Reservoirs. Recently, we have formulated the MFE method to account for capillary pressure contrast in a consistent way. Fig. 3a shows a 2D reservoir with random permeability heterogeneity. Water is injected from the bottom left corner, and oil (and water, after water breakthrough) is produced from the upper right corner. The water-saturation profiles at 0.5 PVI are shown in Figs. 3b (with an average Pc ) and 3c (with Pc effect). Note that it is the contrast in capillary pressure, not an average capillary pressure, that affects flow. There may be no meaning to average capillary pressure.
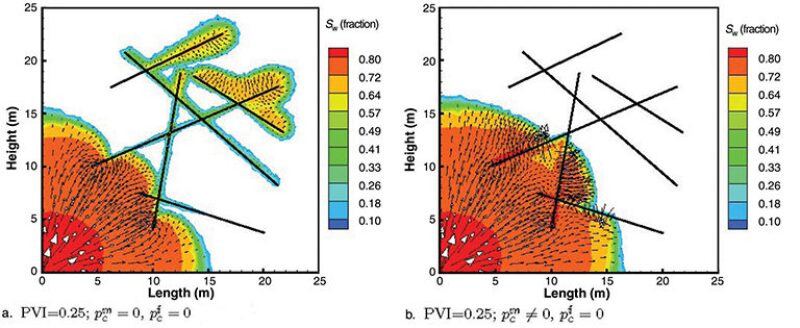
Fractured Reservoirs. There are many problems in fractured reservoirs that may require new methods based on advanced concepts. Some problems cannot be simplified beyond a certain limit. In some fractured reservoirs, for example, diffusion can have a dominant effect on recovery. One may not use binary diffusion coefficients and still hope for accurate results. In this last example, we present saturation profiles for the simple case of water injection in discrete fractured media in 2D. Water is injected at the lower left corner and production is from the opposite top corner. The saturations are shown in Fig. 4. A dual-porosity model could not be used in such a simulation. Results show that the media act as an unfractured reservoir with matrix capillarity, because of capillary crossflow, for the conditions of the example. Injection rate, wettability, and fracture spacing could alter the flow path significantly.
Conclusion
Sometimes in pursuing a solution to a problem, we may move away from the conventional approaches and seek new methods in order to come up with a definitive solution. Our efforts in numerical simulation of fractured petroleum reservoirs not only have resulted in advances in that area but have advanced numerical solution of other complex reservoir problems. That is the fun of research. Such results are extremely rewarding after a period of hard work and concentration, with some luck.
Acknowledgments
We would like to thank K. Ghoryeb, M. Karimi-Fard, and J. Monteagudo, all former post-doctoral researchers at RERI associated with the senior author, who laid the foundation with their research for the results presented in this paper. We also would like to thank member companies of the RERI research consortium and the US Department of Energy for long-term support of the research at RERI.



