Hybrid steam/solvent processes have gained importance as a thermal-recovery process for heavy oils in recent years. Among the identified physical mechanisms that play a role during these processes are heat-transfer phenomena, gravity drainage and viscous flow, solvent mass transfer, and mass-diffusion/-dispersion phenomena. In this paper, a study of sensitivity to grid size is described. Ideally, this work will provide some insight into methodological aspects to be considered when hybrid steam/solvent processes are modeled.
Introduction
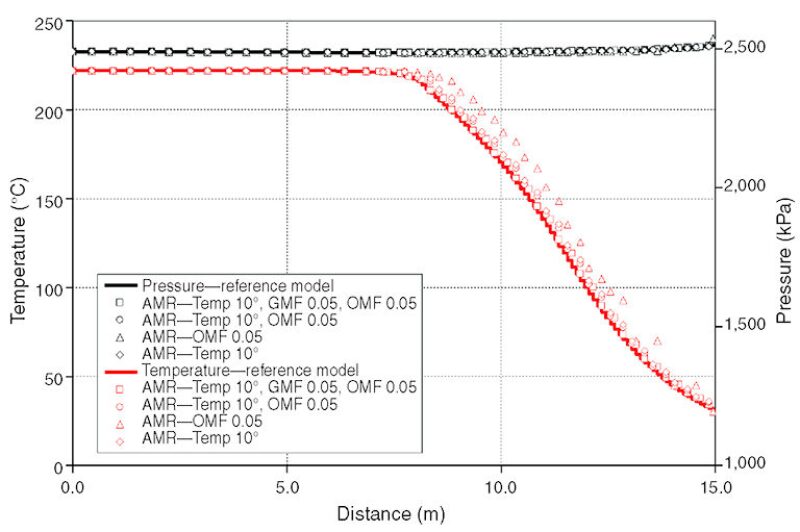
Recent studies concerning the size of the liquid-solvent-rich zone where molecular diffusion and dispersion occur have implied that a detailed representation of the solvent/steam-chamber edge is necessary in the numerical model.