An accurate estimation of viscosity values is imperative for optimal production and transport design of hydrocarbon fluids. Consequently, precise and robust empirical correlation models are highly desired. While the literature contains numerous correlation models, most of these are inadequate for predicting accurate oil viscosity with unbiased data. This paper aims to develop new and improved empirical viscosity correlations through available field measurements on the Norwegian Continental Shelf (NCS).
Introduction
The most-accurate viscosity correlation method makes use of the material balance of compositional information, which implies that a comprehensive pressure/volume/temperature (PVT) report is required. Such PVT reports usually include oil viscosity, which makes the correlation model redundant in many cases. Often, the only information available related to the fluid property is the solution gas/oil ratio (GOR), temperature, American Petroleum Institute (API) gravity, and pressure.
Literature Review
The empirical correlations in the literature have established categories to correlate oil viscosity for dead, gas-saturated, and undersaturated oil. The dead-oil correlations are used to predict the viscosity at standard conditions, when no gas is left in solution. All correlations from the literature express dead-oil viscosity as a function of API gravity and temperature. The second category is defined as a function of dead-oil viscosity and solution GOR and is applied when the fluid is at, or below, the saturation pressure. The latter correlation is normally expressed as a function of saturated oil viscosity, bubblepoint pressure, and reservoir pressure. The undersaturated-oil-viscosity correlations are applied when the reservoir pressure increases beyond the saturation pressure. This study investigates the statistical performance of 10 dead-oil, eight saturated, and five undersaturated oil-viscosity correlations.
Methodology
Traditionally, the correlation models present an explicit mathematical expression based on field measurements to predict viscosity, while this paper presents three different correlation methods. Two methods are recognized as surrogate models to predict the viscosity properties, called the radial basis function network (RBFN) and kriging. In contrast to the traditional correlation models, these techniques do not present a mathematical correlation, because the models make use of a statistical approach with more consideration of the variation in input variables to predict the output. The kriging method demonstrated results superior to those of the empirical correlations. The third and last approach is an optimization algorithm called particle-swarm optimization (PSO). The technique recalculates the coefficients of the discussed correlations from the literature while maintaining the functional form of the expressions.
RBFN. The RBFN is a type of surrogate model in which the inner part of the model is assumed to be unknown because the system is based solely on transfer characteristics (i.e., only the input and output variables have an influence on the model). The aim of the surrogate model is to replace time-consuming and cumbersome simulations and experiments to predict the outcome variables of a known input set.
The network consists of an input vector, a hidden layer with RBFN-reference neurons, and an output layer comprised of a set of single classified nodes. The hidden layer identifies a classification to the N-dimensional input vector, where each neuron compares the input vector with a reference function to compute the degree of correlation ranging from zero to unity, with unity representing a uniform fit. The RBFN makes use of radial basis functions as activation functions.
PSO. This method is a stochastic optimization technique inspired by the social behavior of animals. The PSO is comprised of a swarm of particles moving through the problem space. Each particle is termed as unintelligent, meaning that, as individuals, they are unable to compute a solution; however, the particles are able to obtain a solution through interactions with neighboring particles. The particles have a memory of their personal best solution in the problem space relative to the defined objective function. Furthermore, each particle has a memory of the global best solution of the system, which is the best position any particle has achieved at each timestep. Over a number of iterations, each particle interacts with other particles to change its position according to the objective function.
Results and Discussion
Dead-Oil Viscosity. The performance of the published dead-oil correlations displays a wide span in statistical accuracy. The erroneous behavior could potentially be linked to the fluid database. The dead-oil viscosity is defined at temperature and pressure at standard conditions, while the database presents dead-oil viscosity at atmospheric pressure and reservoir temperature. The PVT data of dead oil, therefore, are considered questionable because the presence of gas is not clearly accounted for and could vary considerably from the authors’ reference samples. The inaccuracy could further originate from the correlation method of dead-oil viscosity, which is solely a function of two parameters. The two-parameter approach is considered problematic because two dead-oil samples may present a large difference in viscosity while having the same API and temperature. The dead-oil viscosity correlations are based further on the assumption that the fluid is characterized as Newtonian.
The proposed correlation model is superior to all established models, improving the correlation results by 39.7% relative to the best original correlation expression. The model should be used with caution, considering the uncertainty related to the questionable PVT data used as reference. However, the physical trends of the correlated dead-oil viscosity correspond well with the general effects of temperature and API gravity. Furthermore, the original models do not present a bias toward the data set, which indicates that the data set does not reflect a consistent deviating trend from the authors’ original reference data.
Saturated-Oil Viscosity. When considering the statistical performance accuracy of the saturated-oil-viscosity correlation models, the empirical response by the proposed model is superior to all discussed models. Eight published correlations were investigated as bases to create an improved prediction model for saturated oil viscosity. The proposed correlation model is modified by keeping the coefficients of the original dead-oil correlation fixed rather than using the modified dead-oil coefficients, even though the latter correlation provides slightly more-accurate results. The correlation is discarded because of the debatable data set used as reference to develop the model, which means this correlation may not truly be an improved estimation model.
The proposed new correlation model presents an improved accuracy of 26.4% relative to the best original correlation model. A low dispersion relative to the reference line is observed throughout the whole viscosity range, with only a few deviating points. The results indicate that the prediction model is in agreement with the true viscosity. The final recalculated coefficients are based on all data; thus, it is reasonable to assume that the modified model presents either the same or an improved, empirical response compared with the stated statistical accuracy. The proposed modified correlation model for undersaturated oil viscosity also presents superior results compared with the original correlations.
Error Analysis. The most-accurate viscosity correlations are the modified work of Bergman, RBFN, and kriging. The different correlations are functions of temperature, API gravity, and GOR. The error analysis was conducted by categorizing temperature and API gravity into high and low subsets, while the GOR and targeted viscosity values are sectioned into specified ranges. On the basis of the sensitivity analysis of temperature, both the RBFN and the modified correlation are little affected by either low or high temperature, while the original model of Bergman presents a highly inaccurate response at temperatures below 190°F. Fig. 1 shows a more-erroneous response in the lower API-gravity range. In general, viscosity increases with an increase of heavy molecular components, such as asphaltenes. The RBFN seems to handle higher viscosity values better than the other correlations.
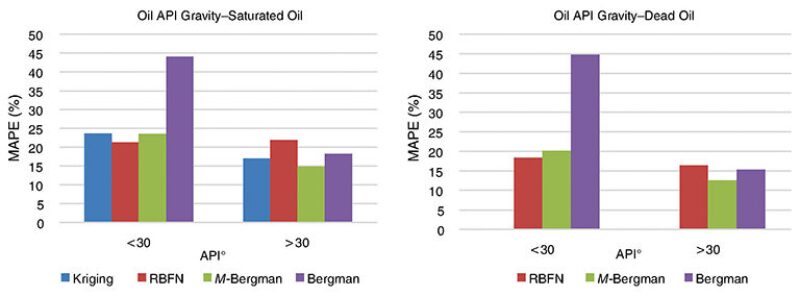
On the basis of the graphical interpretations, the modified correlation model of Bergman presents the most-consistent empirical performance overall because the modified correlation models do not demonstrate any distinctly inaccurate responses at different reservoir conditions. The consistent accuracy adds more confidence that the model is a true improvement over existing correlation models.
Conclusions
This study is based on a comprehensive fluid database representing the range of fluid properties on the NCS. The data set has been thoroughly quality controlled. However, uncertainty is linked to the dead-oil data because of the experimental measurement conditions. On the basis of statistical accuracy, the proposed prediction model for dead-oil viscosity demonstrates a significant improvement over the original correlations. However, discretion is recommended, considering the questionable PVT data used as reference.
The modified correlation model of saturated-oil viscosity demonstrates a higher accuracy than all the presented correlations. On the basis of this performance, one can conclude that the proposed model is a significant improvement to the established correlations. However, it is recommended to use kriging when correlating for saturated oil viscosity, provided that the model is practically available.
This article, written by JPT Technology Editor Chris Carpenter, contains highlights of paper SPE 191296, “An Improved Correlation Approach To Predict Viscosity of Crude-Oil Systems on the NCS,” by Jørgen Bergsagel Møller, SPE, Knut Kristian Meisingset, SPE, and Ibnu Hafidz Arief, Equinor, prepared for the 2018 SPE Norway One Day Seminar, Bergen, Norway, 18 April. The paper has not been peer reviewed.

