Evaluation of Strategies for Enhancing Production of Low-Viscosity Liquids

Production of low-viscosity liquids, including condensates, from tight reservoirs such as shales is severely restricted by the ultralow permeability of such formations, limiting production to a very small fraction, usually less than 5%, of the liquids in place. In this study, the authors evaluate, by means of numerical simulation, several possible strategies to enhance low-viscosity-liquid production from such reservoirs. The objectives of this effort are to remove from further consideration strategies that hold limited promise, and to identify strategies that have potential for further study.

Introduction

The remarkable success of gas production from tight reservoirs and shale reservoirs has not been matched by similar progress in the production of relatively-low-viscosity liquid hydrocarbons (including condensates) because of the significant challenges to liquid flow posed by the ultralow permeability of such reservoirs.

Increasing the recovery of liquids from these ultralow-permeability systems even by 50% over its current very low levels not only will increase production and earnings but will have considerable wider economic implications because the increased recovery will affect reserves and the valuation of companies. The authors’ effort aims to address this issue by using numerical simulation to investigate a wide range of possible strategies for improved liquid production from tight/shale reservoirs. In essence, this is an attempt to provide a baseline mechanistic study that deploys some state-of-the-art tools in reservoir modeling. The paper focuses on determining the baseline performance of various key production methods that are considered standard in the attempt to produce low-viscosity liquids from tight reservoirs and shale-oil reservoirs. These include recovery by use of displacement methods, viscosity-reduction methods, enhanced reservoir stimulation, and combinations thereof.

For a discussion of the simulation code and the underlying fundamental equations of flow and transport, please see the complete paper.

Fractured-System Description and Subdomain Representation

Subdomains. The fractured system in producing tight gas reservoirs and shale-gas reservoirs can be described as a set of interacting subdomains. These include the following:

• Subdomain 1 (S1): The original (i.e., in its undisturbed state before the initiation of production operations) reservoir rock, which may be naturally fractured and may be characterized by distinct sets of fractures, each one with its own properties (aperture, length, orientation, and density). The original fractures in S1 are hereafter referred to as native fractures (NFs).
• Subdomain 2 (S2): The fractures or fractured network created during the reservoir stimulation (e.g., by hydraulic fracturing of the reservoir rock). These artificial fractures penetrate S1, increase the production surface area, and may intercept the NFs of S1, thus providing access to the well for gas in these fractures. The fractures are expected to be the dominant pathways of flow to the well and are referred to as primary fractures (PFs).
• Subdomain 3 (S3): This is the subdomain defined by the stress-release fractures that are induced by changes in the geomechanical status of the rock in the vicinity of the PFs following the reservoir-stimulation process. Their orientation is a function of the stress distribution and geomechanical properties of the rock, but they tend to occur on planes that are roughly perpendicular (or at an angle) to the PFs. Such fractures are referred to as secondary fractures (SFs); they penetrate S1 mainly adjacent to PFs (i.e., they occur within the fracture spacing, and, in their upper limit, they can cover it entirely), and they intercept NFs and PFs, thus increasing the flow area and, consequently, production.
• Subdomain 4 (S4): This is the subdomain defined by the stress-release fractures that are induced by changes in the geomechanical status of the rock in the immediate vicinity of the wellbore because of drilling. S4 is expected to have a roughly cylindrical shape centered around the wellbore axis and to be characterized by a limited radius (i.e., short fracture length), high fracture density, and a small aperture. Thus, S4 is expected to represent a small fraction of the overall system volume, but it may be important to flow because this fracturing can increase the flow area significantly, in addition to being directly connected to S1 and S2 and possibly intersecting fractures in S3. The fractures in S4 are hereafter referred to as radial fractures (RFs).

Thus, S1 is the natural (at discovery) state of the system. Drilling and well installations may inevitably cause S4 to form. S2 is the result of reservoir-stimulation activities (and the only subdomain over which the operator can exert control), while S3 is a direct byproduct of stimulation activities. S1 cannot provide sufficiently high production rates without stimulation in tight reservoirs and shale-gas reservoirs because of their very low permeability. For the same fracture characteristics (except fracture length), production is maximized when the cumulative size of S2, S3, and S4 is maximized.

Types of Fractured Systems. On the basis of the properties and characteristics of S1 and the occurrence (or absence) of S3, there are four possible types of producing tight reservoir or shale-gas-reservoir systems. These are listed in order of increasing complexity (in terms of description, simulation, and analysis).

1. Type I: This is characterized by (a) the absence of NFs in S1, which now involves the unfractured matrix and (b) the absence of the S3 subdomain. This is the simplest and least-productive system because it is characterized by the minimum surface area and flow pathways for production. It is possible to simplify it further by assuming absence of the S4 subdomain and of the RFs.
2. Type II: Unlike Type I, Type II systems feature the S3 subdomain and SFs. This is expected to yield higher gas production because of increased surface area and more pathways to flow. SFs can extend along the entire length of the fracture spacing.
3. Type III: The difference between Type I and Type III systems is the occurrence of the NFs in S1. Such a system is expected to have higher gas production than Type I systems. Comparison of its productivity with Type II is not straightforward because production is controlled by the characteristics of the fractures and the relative contributions of NFs and SFs cannot be determined a priori.
4. Type IV: This system involves all four subdomains and all fracture types (NFs, PFs, SFs, and RFs). This is the most complex system to describe, simulate, and analyze. All other features and characteristics being equal, this is clearly the system with the highest production potential because it has the maximum (compared with the other types) surface area and the largest number of flow pathways to the production well.

For a discussion of the simulation approach, system properties, boundary conditions, and the numerical treatment of the fractured subdomains, please see the complete paper.

Results and Discussion

Reference Cases. The authors consider two reference cases. The first case (Case R) involves only the native S1 system, and represents the unstimulated formation. The second reference case (Case RF) involves a stimulated system with hydraulically induced fractures (i.e., it comprises the S1 and S2 subdomains). The dimensions of these two systems are listed in Table 1 of the original paper.

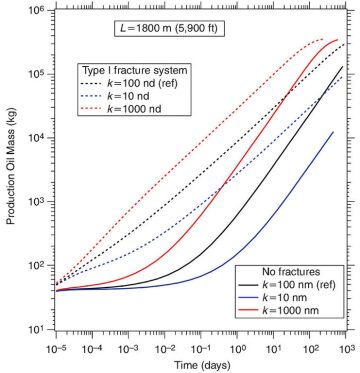
Fig. 1 above shows the mass rate Q of light-oil (having the properties of n‑octane) production in Cases R and RF, and Fig. 2 shows the corresponding cumulative mass M of produced light oil during the same period. Additionally, Figs. 1 and 2 include the evolution of Q and M for various levels of matrix permeability. The effect even of a single fracture (the PF in Case RF) on Q and M is shown to be rather dramatic, increasing their early levels by at least an order of magnitude over those in Case R. This holds true for every level of matrix permeability. As expected, higher matrix permeability corresponds with higher early Q and M, although this cannot be expected to last for the entire duration of production because the amount of oil in the system is fixed and the same in all cases.

Gas-Displacement Processes. Fig. 3 shows the Q corresponding to a continuous gas drive obtained by maintaining the upper well at a constant bottomhole pressure P_w=2×10⁷ Pa in Cases R and RF. The authors used two different gases, methane (CH₄) and nitrogen (N₂). Despite expectations of a better performance with the CH₄ drive, the results for the two gases were practically the same. This was attributed to the fact that the invading CH₄ is acting mainly as a displacement agent, and its advancing front does not have the opportunity to effect a change in viscosity and, consequently, an increase in production.

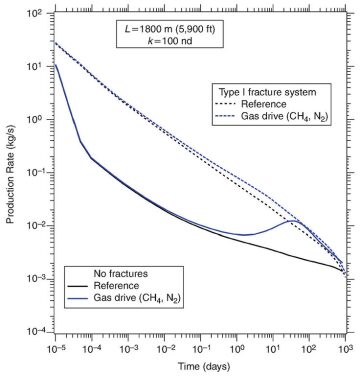
The results in Fig. 3  indicate that gas displacement does have a positive impact by increasing Q. Its effects become evident earlier in Case RF because of the light-oil displacement into the hydraulic fracture in the vicinity of the injection well. The increase in Q becomes evident later in the nonfractured system of Case R, but the effect of displacement is more pronounced than that in Case RF. However, it is interesting to note that the gas-displacement process can at a later time compensate (at least partly) for the absence of the PF. How­ever, there is evidence that the positive effects of displacement are accompanied by an undesirable change in the relative permeability of the oil once the gas front reaches the production well.

Thermal Processes. The authors investigate the effect of heating to effect a reduction in the viscosity of the light oil, and the overall effect of heating on gas production. The authors have two heating cases in each of the systems: Case R-H1 involves heating that begins at the time of production, while Case R-H2 involves heating for an entire year before the beginning of production. Cases RF-H1 and RF-H2 are analogous. Heating is accomplished by flowing a fluid at a constant temperature T_H=95°C in the upper well.

The positive effects of heating are limited in Cases R-H1 and RF-H1, and they appear quite late in the production process. This was expected because of the reliance on the very slow method of heat conduction through the matrix, which does not allow fast heat transfer from the upper well toward the rest of the formation. The situation is significantly different in Cases R-H2 and RF‑H2. In these cases, the increase in Q is significant (i.e., by a factor between two and three over the nonheated cases). However, this has to be considered with respect to the economic implications of continuous heating for an entire year without production. The heating positive effect on Q is more pronounced in the presence of the PF because of the ability of flow into both the fracture and the well. Additionally, the heating effect cannot compensate for the absence of a fracture in the unfractured system, the Q of which is lower than that for the fractured system.

NFs and/or SFs. The authors investigate the effect of the presence of NFs or SFs on Q. Addition of such fractures to Case RF changes it from its original Type I status into a Type III system. Case R is now enhanced with an NF system. In both cases, the NFs are represented as a 3D system with a fracture density of 1 fracture/m, with fracture aperture of 0.1 mm, and the domain is simulated using the microbiologically-influenced-corrosion concept. The results indicate that the addition of the NFs has a dramatic effect on production, which increases by several times over that of Cases R and RF. The impact is more pronounced in Case R.

This article, written by JPT Technology Editor Chris Carpenter, contains highlights of paper SPE 169479, “Evaluation of Strategies for Enhancing Production of Low-Viscosity Liquids From Tight/Shale Reservoirs,” by G.J. Moridis, SPE, Lawrence Berkeley National Laboratory, and T.A. Blasingame, SPE, Texas A&M University, prepared for the 2014 SPE Latin American and Caribbean Petroleum Engineering Conference, Maracaibo, Venezuela, 21–23 May. The paper has not been peer reviewed.