Modeling Transient Wellbore Temperature During Diagnostic Fracture Injection Tests

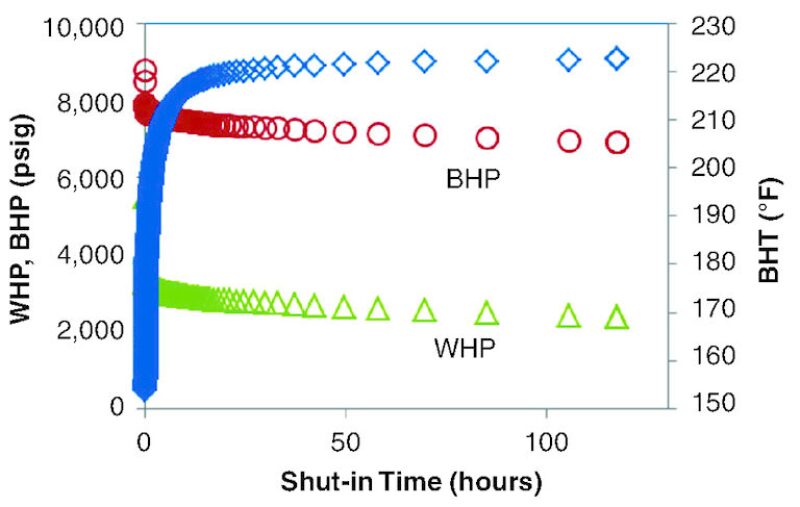
Diagnostic fracture injection tests (DFITs) have gained widespread usage in the evaluation of unconventional reservoirs. In typical field operations, pressure is measured at the wellhead, not at the bottom of the hole. The bottomhole pressure (BHP) is obtained by adding a constant hydrostatic head of the water column to the wellhead pressure (WHP) at each timestep. One can question the soundness of this practice because of significant changes in temperature that occur in the wellbore, leading to changes in density and compressibility throughout the fluid column.