Naturally fractured reservoirs (NFRs) contain a significant amount of remaining petroleum reserves and are now being considered for water-alternating-gas (WAG) flooding as secondary or tertiary recovery. The authors face the challenge of reservoir simulation of WAG by building models at various scales, starting with pore scale and expanding to an intermediate scale and then to reservoir scale. They show how pore-network modeling and fine-grid modeling where the fractures and matrix are represented explicitly can be used to increase the accuracy of numerical simulations at field scale.
Introduction
A significant portion of the world’s remaining petroleum resources is located in NFRs, including supergiant fields in the Middle East. A detailed understanding of the recovery processes involved in extracting hydrocarbons from NFRs by use of enhanced-oil-recovery techniques is key to increasing ultimate recovery for such reservoirs.
Waterflooding has been used with various degrees of success in NFRs. For unfavorable (i.e., mixed- to oil-wet) matrix wettability, however, waterflooding can be ineffective.
Gas/oil gravity drainage (GOGD) provides an important drive mechanism that can be effective irrespective of the rock wettability. In NFRs, fractures increase the exposure of the injected gas to oil in reservoir rock, which renders GOGD more effective than it is in unfractured reservoirs. Consequently, gas injection has been applied in many NFRs. However, because the gas mobility is very high compared with that of water and oil, so is the risk of bypassed oil and gravity override, which can lead to very early gas breakthrough. This is particularly true for NFRs.
WAG flooding combines the merits of the two injection fluids on macroscopic and microscopic scales while stabilizing the injection front, delaying breakthroughs, and, therefore, leading to increased oil recovery compared with continuous water or gas injection.
Reservoir simulation of WAG injection is very challenging because a representative three-phase saturation model is required to predict relative permeability and capillary pressure as water and gas saturations increase and decrease alternately. Three-phase relative permeability and capillary pressure data are extremely difficult to measure experimentally. Even if experimental evaluation becomes feasible, an infinite number of saturation paths can occur in the reservoir. This necessitates the use of empirical, or interpolation, models to predict three-phase relative permeability and capillary pressure from two-phase experiments.
In NFRs, capillary pressure and relative permeability functions have a major effect on fluid exchange between matrix blocks and fractures. Predicting the effects of the interplay of viscous, capillary, and gravity forces is challenging because fluid flow is viscous-dominated in the fractures while transfer between fractures and matrix blocks is dominated by capillary and gravity forces. Because most of the oil is contained inside the matrix, capillary and gravity forces can be more important in NFRs than in conventional reservoirs.
This capillary-/gravity-driven exchange between fractures and matrix is commonly modeled by use of dual-porosity or dual-porosity/dual-permeability models.
The authors use a novel pore-network model to predict three-phase relative permeability and capillary pressure functions of arbitrary wettability to model fracture/matrix transfer processes during WAG flooding. While it is difficult, time consuming, and costly to obtain all hysteretic two- and three-phase relative permeability and capillary pressure functions experimentally for the same rock sample, pore-network models can generate a complete saturation function for the same pore structure.
The authors attempted to preserve small-scale recovery processes at the field scale to ensure that they were well represented in porosity models. Therefore, they introduced a stepwise upscaling procedure () to preserve these processes across various scales.
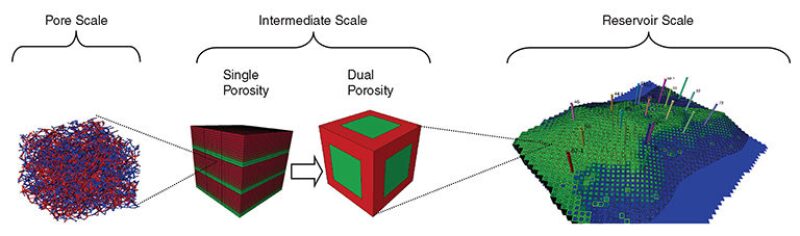
Pore-Scale Displacements To Predict Saturation Functions
The authors’ three-phase pore-network model accounted for all observed microscopic displacement processes during three-phase flow, such as multiple displacement chains, layer formation and collapse, or film flow. The pore-network simulator has been benchmarked against published three-phase experiments for sandstones and micromodels of different wettability.
To generate relative permeability and capillary pressure data, the network was initially saturated with water followed by oilflooding to simulate a primary-drainage process. Then, a series of waterflooding (imbibition) simulations followed until the network water saturation reached a predefined value, at which gasflooding commenced (Fig. 2).
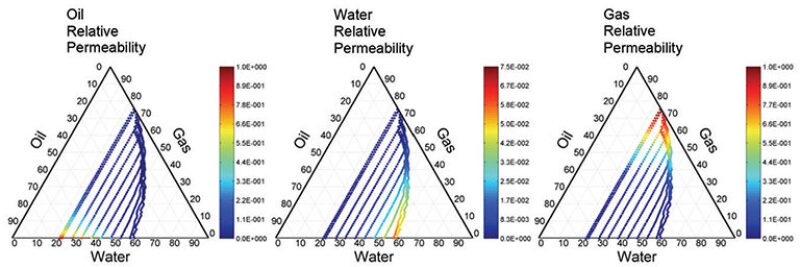
The Intermediate Scale
A fine-grid model was constructed to investigate the effect of three-phase relative permeability and capillary pressure on matrix/fracture transfer for a gridblock scale of 50×50×50 ft with 27 (3×3×3) matrix blocks that are 12×12×12 ft each. This resembles the classical but highly idealized sugar-cube array (Fig. 3). This model allows for results from the pore scale, in the form of relative permeability and capillary pressure tables, to be brought to the continuum scale where fractures and matrix are present. To simulate WAG cycles, the fractures were instantly filled with water or gas when modeling recovery from the 27 matrix blocks. Matrix blocks were assigned two- and three-phase data. For the fractures, linear relative permeability was used and zero capillary pressure was assumed.
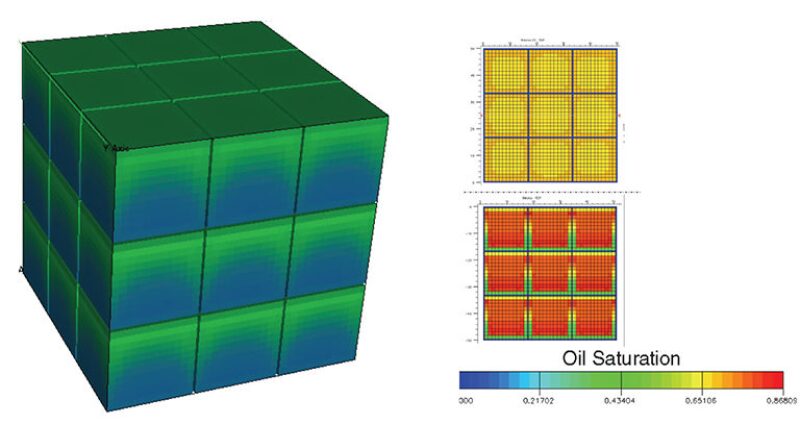
During the first two water/gas cycles, recovery predicted for all empirical models reasonably matches recovery predictions for the pore-network-derived three-phase relative permeability and capillary pressure. This is because the total average oil saturation is relatively high and, hence, close to two-phase relative permeability and capillary pressure curves. However, empirical models predicted that oil recovery continues to increase in subsequent WAG cycles whereas the pore-network-derived functions predicted no substantial increase in oil recovery after the first two flooding cycles. This is because relative permeability and capillary pressure functions from the pore-network model cause water and gas phases to displace each other but do not recover additional oil, leaving the oil phase undisplaced.
WAG-Flooding Sensitivities
On the basis of the pore-network-derived saturation functions, the authors considered a series of sensitivities to WAG-flooding-design parameters—WAG-cycle duration and -cycle order—as well as the effects of altering the matrix wettability.
Cycle Duration. For the nonviscous-dominated flow between matrix blocks and fractures, the authors observed that the overall WAG recovery exhibited little to no sensitivity to the WAG-cycle length. However, the results also show that the shorter the WAG cycle, the higher the speed of recovery. This is because most of the oil is produced during the first two water/gas cycles because of a combination of water imbibition and gas gravity drainage. During later WAG cycles, little additional oil recovery is achieved when using pore-network-model-derived relative permeabilities.
Cycle Order. The order of WAG cycles also has an effect on oil recovery from the matrix. At first, oil displacement by spontaneous water imbibition occurs faster than GOGD if the matrix is water-wet. Then, recovery by water imbibition begins to diminish because of the reduction in oil-phase mobility as water saturation increases at the boundaries of matrix blocks. Gas-gravity-drainage displacement continues to increase and eventually outperforms recovery by spontaneous water imbibition. The difference in recovery profiles during gas and water injection for the WAG cycles is an indication of the competition between the phases. This is because, when gasflooding occurs after waterflooding, the average initial water saturation is high. Hence, oil recovery is slow in the beginning because gas displaces water first. The water cycle follows the same explanation.
Effect of Matrix Wettability. The rock-matrix wettability has a significant effect on recovery from NFRs. To study this effect, three-phase relative permeability functions, capillary pressures, and saturation paths were recomputed with contact angles adjusted to represent oil-wet rock. As expected, water/oil capillary pressure values were negative in the oil-wet case. This dramatically changes the efficiency of water injection for recovering oil from matrix blocks; capillary forces act against water entering the blocks. However, gravity forces, because of the density difference between the water and oil phases, enable the water phase to start displacing oil in the matrix blocks from the bottom up. Recovery from water displacement by gravity alone in oil-wet reservoirs is significantly less than that from the combined gravity and capillary forces in water-wet reservoirs. However, water gravity displacement in an oil-wet reservoir is a cocurrent displacement and does not lead to the trapping of oil inside blocks by the low-oil-mobility region.
Discussion and Concluding Remarks
The application of three-phase saturation functions showed that the empirical interpolation methods to estimate three-phase saturation functions, which are commonly used in standard industry simulation practice, overestimated oil recovery during late WAG cycles by an absolute difference of 25% compared with physically consistent and pore-network-derived relative permeability and capillary pressure functions. The authors suggest that the reason for such a tremendous difference is the more accurate representation of intrapore displacement processes in relative permeability and capillary pressure functions that are computed from pore-network simulation. A sensitivity analysis revealed that water imbibition during the water-injection cycles in WAG flooding creates a region of low oil mobility around matrix blocks. At such low oil saturations, empirical interpolation models over-estimate relative permeability, predicting more oil to be released from the center of matrix blocks.
The sensitivity analysis also showed that recovery speeds up with decreasing length of WAG-flooding cycles but that final recovery always converged to a similar value. Final recoveries were also similar for cases in which the order of the WAG cycles was changed. Surprisingly, continuous gas injection in water-wet rocks yielded higher oil recoveries compared with WAG flooding, whereas continuous water injection recovered less oil compared with WAG. Hence, the authors concluded that water imbibition has an adverse effect on recovery from matrix blocks if gas is available for injection. This is because of the low-oil-mobility region at the fracture/matrix interface.
The authors point out that the results cannot be used to evaluate WAG-flooding success in general because viscous displacement is not taken into consideration. The question, therefore, remains: Will heterogeneity in the viscous flow field, arising from nonuniform fracture networks, dominate recovery or will uncertainty in the fracture/matrix transfer prevail and control the overall recovery behavior during WAG?
This article, written by Special Publications Editor Adam Wilson, contains highlights of paper SPE 164837, “Multiscale Simulation of WAG Flooding in Naturally Fractured Reservoirs,” by Mohamed Ahmed Elfeel, Adnan Al-Dhahli, Sebastian Geiger, SPE, and Marinus I.J. van Dijke, Heriot-Watt University, prepared for the 2013 EAGE Annual Conference and Exhibition/SPE Europec, London, 10–13 June. The paper has not been peer reviewed.
