As a petroleum engineer, deciding how to drill for, extract, and transport petroleum is part of the job. These decisions and others are often mutually exclusive in nature. One must decide between opportunities based on revenue (making an Income Analysis) or spending the least amount of money (requiring a Service Analysis).
Either way, an effective economic model is necessary to maximize your profit. Net Present Value (NPV) and Rate of Return (ROR) are common criteria relied upon to make these economic evaluations; but chances are, each could you lead you to a different conclusion as to which opportunity is the best choice for your company.
Let’s explore an example to evaluate NPV and ROR. Assume you have two mutually exclusive investing opportunities with differing cash flows, NPVs and RORs. Project A offers a 25% ROR, and Project B offers a 15% ROR. Your job is to choose which project is the best investment for your company. While a higher ROR seems like a simple justification for choosing one project opportunity over the other, a cash flow model is invaluable to make a fully informed decision.
The following cash flow models lay out the individual cash flows for each project. Assume a minimum ROR of 10%.
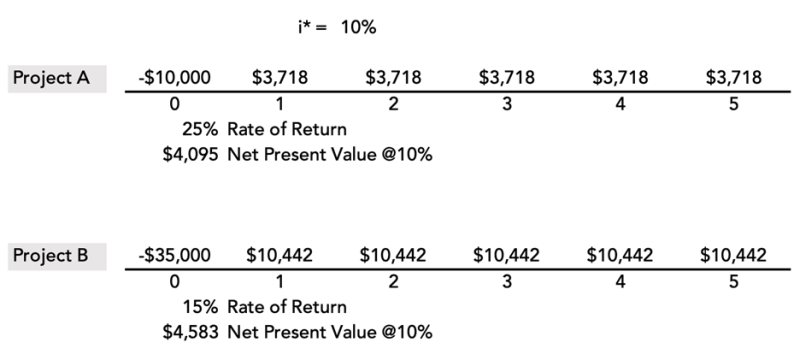
Choosing projects based on ROR is common industry practice, and given our minimum ROR of 10%, it seems obvious that a higher ROR of 25% is the clear winner. However, if you make decisions based on NPV, you would choose Project B with the higher NPV at $4,583.
The two most common economic criteria are not in agreement, so which one should you rely on to make an economic decision? Could more money be made by choosing the larger NPV?
The short answer is that both can be used, but only if an incremental model is made. An incremental model should be structured to evaluate the economic value of the additional money invested in a more capital-intensive alternative.
The incremental analysis forces you to ask where the $25,000 ($35,000-$10,000) might be invested if Project B is selected. If the smaller investment associated with Project A is selected, the baseline assumption is the extra $25,000 will go into other projects earning a 10% minimum ROR and a zero NPV. What if the extra $25,000 was put into the larger capital investment Project B?
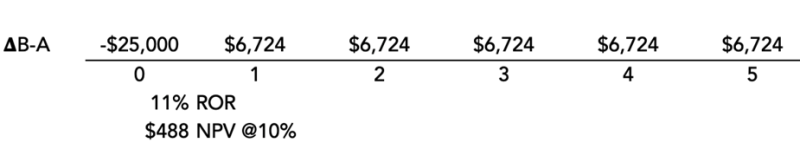
By taking the difference between the two options, you can see that the extra $25,000 should be invested in Project B and not in other investment opportunities at 10%. Additionally, by investing in Project B, you are creating $488 of additional value, even though it has a smaller ROR of 15%.
Comparing RORs is extremely common but not always accurate. The following example is helpful to remember this fundamental evaluation concept.
If someone offered you an investment opportunity with a 10% ROR or a 100% ROR, which one should you choose? Standard industry practice would lead you to select a 100% ROR. But what if I told you the 100% ROR was on $1.00 and the 10% ROR was on $1,000? This information leads people to switch to choosing the smaller ROR on more money invested.
Let me address two rebuttals that we often get in response to the above scenario. You might be thinking that undertaking three versions of Project A would be most beneficial to your company for the money you have to invest. However, you are no longer thinking of these projects as mutually exclusive. They would fall under the Non-Mutually Exclusive Rules for project evaluation where more than one project can be selected. You may also be considering an option to find a project to invest the extra money at, say, 20%.
Economic models are only as good as our assumptions going into them. The motto “garbage in, garbage out” comes to mind. The minimum ROR should reflect the other opportunities you have now and in the future. If 20% is your minimum ROR, then it is necessary to re-evaluate these mutually exclusive alternatives at 20%. For the assumed higher minimum ROR of 20%, Project B is undesirable with only a 15% ROR, leaving Project A as the desired opportunity.
In the end, it’s important to remember that one should never compare two project RORs head-to-head to make a mutually exclusive decision. When properly developed, an incremental evaluation will cause all criteria, including ROR, NPV, and ratios, to reach the same economic conclusion.
Our company has been teaching economic evaluation techniques that are vital to the success of your business and financial well-being since 1972. If you haven’t already taken our course, Economic Evaluation & Investment Decision Methods, register today for a public course offered at Colorado School of Mines in Golden, Colorado.
Upcoming 2024 public course dates are: 10–13 June, 15–18 July, and 4–7 November. In addition to these, we offer public courses at Midland College in Texas, October 14-17.
If you have a group of engineers, geologists, landmen, or anyone else who should understand how economic decisions are made, we can tailor an in-house course to fit your evaluation needs. Our course is also available online in an asynchronous format.
Visit our website for a detailed course description and to learn which one of our course offerings is best for you.
We look forward to having you in class!




