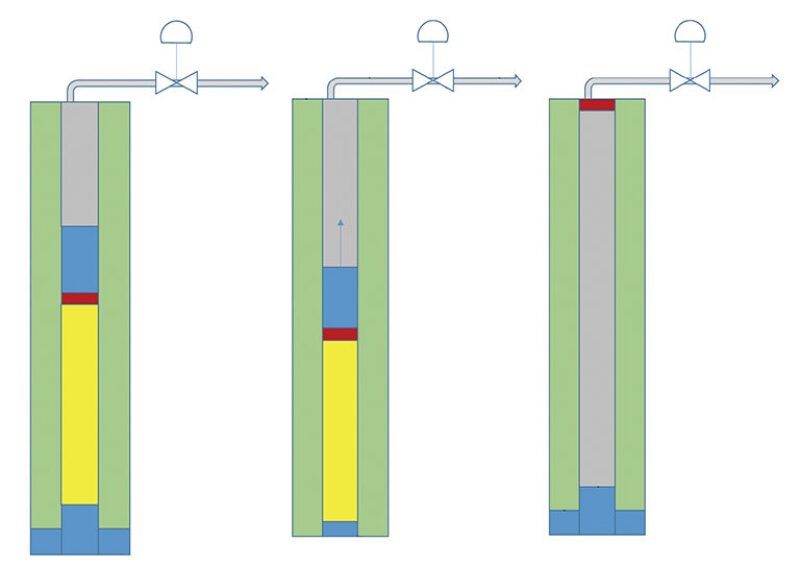
Natural-gas wells suffer from liquid loading if the gas-flow rate is insufficient to carry liquids to the surface. Because of the technique’s many advantages, plunger lift has been used widely in gas wells for the removal of liquid columns and the rescue of dying gas wells from liquid loading. Existing plunger-lift models in the literature are imperfect either because of limited field applications or oversimplified assumptions. Several components in the cyclic movement of a plunger can be identified, with each comprising a set of specific governing equations.
×


Continue Reading with SPE Membership
SPE Members: Please sign in at the top of the page for access to this member-exclusive content. If you are not a member and you find JPT content valuable, we encourage you to become a part of the SPE member community to gain full access.