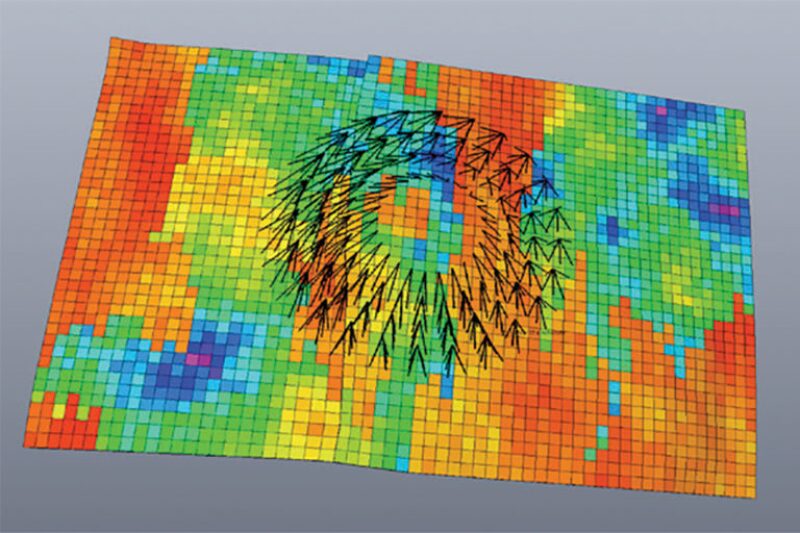
Well-placement optimization is one of the more challenging problems in the oil and gas industry. Although several optimization methods have been proposed, the most-used approach remains that of manual optimization by reservoir engineers. The work flow proposed here uses a machine-learning algorithm trained on simulated data to evaluate the performance of possible well locations and configurations.
Introduction
Extensive literature has been published about well-placement optimization; authors have proposed many different approaches (e.g., advanced optimization techniques, adjoint methods, experimental design, and streamline solutions). Real field experience, however, has shown that these techniques are rarely used. In practice, expert engineers usually identify the main factors affecting a future well’s production.