The design of subsea equipment for pressures greater than 15,000 psi and temperatures more than 250°F is a substantial challenge. The current standard from the American Petroleum Institute (API), Specification 17D, for designing subsea equipment provides little guidance on conditions exceeding these measurements. This work has been performed to demonstrate the acceptance of existing methods for high-pressure/high-temperature (HP/HT) conditions and introduce advanced American Society of Mechanical Engineers (ASME) methods for designing subsea equipment.
Introduction
The design methods given in API 17D refer to the design methods of API 6A, which are valid for working pressures up to 20,000 psi and temperatures up to 650°F. The ASME Boiler and Pressure Vessel Code (BPVC), Section VIII, Division 2 and Division 3, provides design methods for high-pressure vessels. These design methods must meet the API allowable limits and material and test requirements. ASME BPVC has its own design material and test requirements to be used along with the design methods outlined in the ASME codes. A design method combining the ASME design techniques with API material and test requirements that satisfies both the codes is desirable. An example evaluation is presented of an API 17D (API 6A, 4-in. 20K) flange flow loop for a design pressure of 20,000 psi and a temperature of 350°F with external tension and bending loads.
The ASME BPVC was a result of a committee set up in 1911 to formulate standard rules for the construction of steam boilers and other pressure vessels. This code is formulated for pressure vessels in the nuclear industry, and for designing storage and transportation tanks. API 17D was formulated for standardization of subsea production systems.
The ASME and API codes differ in material, hydrostatic-test, and nondestructive-examination (NDE) requirements in particular. The API codes provide temperature derating factors for elevated-temperature design. The standard hydrostatic-test requirement per API 17D is 1.5 times the rated working pressure, whereas in BPVC, Section VIII, Division 2, the hydrotest requirement is 1.43 times the working pressure. Additionally, the hydrostatic test pressure in ASME varies between divisions and has also fluctuated over time.
Design Method
Our design methods include (a) linear and elastic-plastic protection against plastic collapse, (b) linear and elastic-plastic protection against local collapse, (c) protection against cyclic loading, and (d) closure and critical bolting design.
To ensure that all modes of failure are addressed, three load cases should be considered: (a) a hydrostatic-load case with a test-pressure value of at least 1.5 times the rated working pressure per API 17D requirements; (b) a working-load case with appropriate load scenarios and temperature distributions as given by the design code used for calculations; and (c) a maximum-load case for each component or assembly, evaluated for stress and structural stability. Along with each of the three load cases listed, each part must take into consideration any fatigue effects on the design.
Protection Against Plastic Collapse. Linear Methods. For temperatures greater than 250°F, thermal analysis will consider temperature distributions and thermal strains. Numerical-analysis techniques such as the finite-element method will determine the stresses in equipment where handbook solutions cannot be applied appropriately.
In vessels that are R/t<4, the classification of stress should not be used (R=inner vessel radius; t=vessel thickness). Stresses may still be linearized, but all results should be considered as primary membrane stresses. If stress linearization is used, the peak stress intensity derived through calculations cannot exceed yield strength for more than 5% of the section thickness (path distance). Thermal loads, when considered in the analysis, can be classified directly as secondary stresses regardless of the R/t ratio. In many scenarios, this will lead to a nonconservative load case; thus, a load case with no thermal loads will also need to be evaluated to ensure design acceptability.
Finite-element methods should use the small displacement theory. Thermal loading or thermal results can be calculated separately or together with the structural model, depending on the particulars of the problem.
Elastic-Plastic Method. The elastic-plastic method can be used to evaluate components and interactions for protection against plastic collapse. The von Mises yielding criterion and associated flow rules will be used. Material data will be reported as true stress/true strain. Actual material-test data for the elastic-plastic methods are preferred, but a standard (and conservative) estimation of material behavior is given in BPVC, Section VIII, Division 2, Part 3. If the capacity of a component under engineering evaluation is to be established using the elastic-plastic methods, the load-case inputs shall be uniformly increased until the solution is nonconvergent.
After evaluating the component or assembly for protection against plastic collapse, further evaluations must be made to protect against local collapse.
Protection Against Cyclic Loading. After evaluation for general and local collapse, further evaluation may be made to determine that a failure mode generated by load fluctuations is not encountered. Examples of these failure modes include fracture formation and ratcheting of nonintegral connections.
In most cyclic-load cases for pressure-controlling or containing equipment with high internal fluid temperatures, it is observed to have more allowable design cycles than the same component evaluated for conditions without temperatures. This is typically observed because of compressive stresses developed at the internal surfaces because of the temperature gradient. Hence, it is important to evaluate the component at a load case with no thermal conditions to ensure design acceptability.
Closure-Bolting Design. Linear elastic methods outlined in API 17D, and paralleled in BPVC, Section VIII, Division 2, Part 5.7, are recommended for closure-bolting design. In analyzing the stress capacity of closure bolting, the maximum allowable tensile stress should be no more than 83% of the material’s yield based upon the root area of the thread.
Both closure and critical bolting require a preload to a high percentage of the material’s yield strength. Closure bolting of all API 6BX and 17SS flanges is to be made up to approximately 67% of the bolt’s material yield stress. Other studs, nuts, and bolting used on end connections of subsea equipment will be made up to at least 50% of the bolt’s material yield stress. Structural bolting is to be made up to the manufacturer’s written specification.
High-strength alloy steel bolts, studs, and nuts will be evaluated for cyclic operation using elastic-stress analysis and equivalent stress-amplitude loading established in BPVC, Section VIII, Division 2, Part 5.5.3 and Annex 3. In cases where loading is shared between components that have deformed, the controlling stress for the fatigue evaluation will be the effective total equivalent stress amplitude (one-half of the effective total equivalent stress range calculated for each cycle in the loading histogram).
As a safeguard to prevent fatigue failure of threaded components, a limit will be placed on equipment so that no regular load encountered during working conditions causes a separation of the clamped joint of a threaded fastening system. An exception to this would be an extreme scenario, such as a drive-off or impact event.
Application
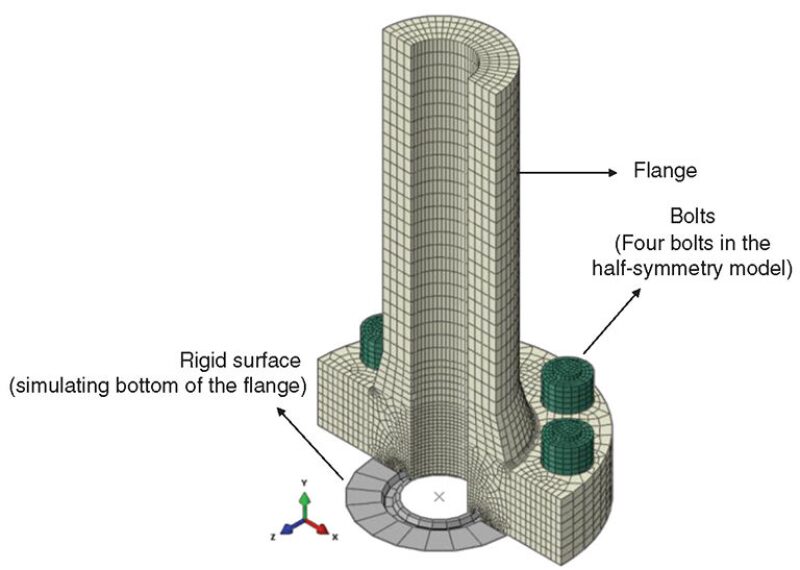
During the writing of this paper and the analysis of an example flange (API 6A, 4-in., 20-ksi, 350°F type 6BX; see Fig. 1, and for analysis results see the complete paper), an experienced senior analyst was used for approximately 2 months. During this period, approximately 8 days were spent on the linear-elastic and fatigue portion of the work, while approximately 60 days were spent on the elastic-plastic and fracture-mechanics portion of the work. With both methods providing approximately similar results in both overall capacity and cycle life, the primary difference was a 650% increase in manpower needed to perform the elastic-plastic and fracture-mechanics analysis. Even with the analyst’s experience, the elastic-plastic analysis results were often subjected to numerical instability, boundary-condition influences, and interpretation of a point of “nonconvergence” because of unbounded deformation.
These results must be accounted for during the planning of a work package for which elastic-plastic and fracture-mechanics analysis is required or anticipated. With the proliferation of finite-element-analysis (FEA) software and the easy-to-use programs, the generation of results has become trivial. However, the burden of establishing if a component is safe shifts from the design engineer to the analyst.
Given the geometries associated with pressure-containing equipment rated for greater than 15,000 psi, the classification and treatment of stress need to be evaluated carefully. In many cases, the elastic-plastic methods referred to previously are the only appropriate tools for the definition of component capacity. This is because, for heavy-walled vessels, especially around local or discontinuous regions, stress linearization is not appropriate. It has also been observed that when large thermal gradients (stresses) are classified as secondary stresses, the capacity charts indicate the increase in capacities because of higher design allowables for the secondary stresses. However, it should also be noted that, for the evaluation of more-standard load cases, the linear-elastic methods provide equally conservative results. Both methods can be used together to provide efficient answers.
Reviewing fatigue and fracture-mechanics analysis for cyclic loading, both methods provide approximately equal results for allowable design cycles. The primary contrast between the methods lies in the material data requirements. Fracture mechanics requires more material testing and characterization, even between the same material batches, while fatigue analysis relies on more generally accepted material assumptions with larger safety factors.
Sample Analysis Results
The linear-elastic and elastic-plastic methods of analyzing the example flange gave the same pressure rating when only internal pressure load was applied. The overall capacity of the flange for the hydrostatic test condition is limited by a bolt that is analyzed using linear-elastic methods. When external loads are used to determine the combined structural pressure/tension/bending-moment capacity of the flange at 350°F, it is observed that the linear-elastic methods give the most-conservative results.
Fatigue and fracture-mechanics analysis for cyclic loading is reported for the identified load cases on the pressure/tension/bending-moment chart at 350°F (refer to figures in the complete paper). The reported cycles show that the flange design has a cyclic-loading capacity that meets the standard cycle requirements (200 cycles) for subsea equipment, but this design should be carefully evaluated for higher-cycle applications.
Conclusions
Existing API methods are adequate for working pressures up to 25,000 psi and temperatures up to 400°F (a limit based on material data availability). The recommendations presented in this paper are not meant to act as a new standard, and an in-depth analysis should be performed on each component or assembly to verify that the proper requirements are met.
This article, written by JPT Technology Editor Chris Carpenter, contains highlights of paper OTC 23928, “A Design Method Combining API and ASME Codes for Subsea Equipment in High-Pressure/High-Temperature Conditions,” by Parth D. Pathak, Christopher G. Kocurek, and Samuel L. Taylor, Cameron International Corporation, prepared for the 2013 Offshore Technology Conference, Houston, 6–9 May. The paper has not been peer reviewed. Copyright 2013 Offshore Technology Conference. Reproduced by permission.
