As the need for oil and gas equipment working in hotter and higher-pressure environments continues to mount, the effort to develop an adequate set of design, material, and validation practices continues to be challenging. More-rigorous stress analysis and design methods that more closely model fast-fracture burst conditions are needed to achieve safe, reliable, and cost-effective equipment designs.
Introduction
As oilfield equipment is subjected to more-severe and longer periods of cyclic forces (internally from irregular wellbore flowing conditions or externally from metocean conditions), many agree that fatigue life and monitoring for these conditions has to be a part of the design equation. This fact is mentioned in the American Society of Mechanical Engineers (ASME) Boiler and Pressure Vessel Code, recognizing the two failure modes of a pressure vessel: leak before burst or a fast-fracture burst. Many oilfield design guidelines negated a need for fatigue analysis because of the long-standing practice of keeping maximum design loads and stresses well below two-thirds material yield strength, a practice that also keeps cyclic-loading issues well inside the “infinite” region on S/N curves in most cases. Unfortunately, this quasistatic design philosophy grows less accurate as the pressure vessel’s wall thicknesses grow or geometries become more complex when addressing high-pressure/high-temperature (HP/HT) conditions. As a result, many have turned to the ASME Boiler and Pressure Vessel Code for guidance. Divisions 2 and 3 of the ASME Code present alternative design methodologies to be considered as internal pressure and temperature increase. However, the designer, using the code, is still free to select which division to follow for his application.
The American Petroleum Institute (API) has long followed a subset of Division 2 of the ASME Code, but it now recognizes many shortcomings as one considers HP/HT conditions. The published technical report only cites the current state of the art and discusses the issues to be tackled. Many observers agree that leaving the issue to so-called “sound engineering judgment” would result in many variations of opinion between operators and manufacturers, likely resulting in inefficiency and repeated tasks. Current efforts address two options: extending current API design practices to higher pressure ratings or establishing a demarcation when different design practices are needed.
Once the designer crosses from Division 2 to Division 3, the scope and duration of design calculations, the qualifying of materials with mechanical performance at higher temperatures and more-corrosive environments, and the number of validation tests and individual test times of HP/HT hardware would increase exponentially. However, this is not a hard and fast rule; again, ASME leaves the choice between Divisions 2 and 3 to the designer.
Pressure-Vessel Design
API 6A describes two methods of verifying the design of bodies, bonnets, and end connections: linear-elastic-stress analysis and the distortion-energy theory. Linear-elastic-stress analysis involves manual calculations or computer analysis to determine stress levels, followed by stress categorization and comparison with allowable stress limits to determine if a particular design is sufficient. However, ASME VIII Division 2 itself spells out the limitations of this method, explaining that it should not be used for heavy-wall pressure vessels because it can yield nonconservative results. It also states that this method is not accurate for complex geometry or complex loading. ASME VIII Division 3 limits the use of this method to thin-wall construction.
The distortion-energy theory refers to a method of equating stress to the amount of energy stored in an elastically deformed material. This verification method is applied solely at the hydrostatic (shell) test pressure condition. The theory assumes that if the part does not yield at test pressure, then it will operate properly at the rated working-pressure condition. The drawback with this method is that it is intended for simple geometries. Structural discontinuities and stress concentrations are beyond its scope, and certain designs may result in localized areas of yielding at structural discontinuities. HP/HT applications compound the problem because of material-strength derating. The test pressure is performed at room temperature, where the material strength is greater, while at operating pressure, the material strength is progressively weaker as the operating temperature increases. Therefore, for equipment to be operated at HP/HT conditions, we do not have the same margin of safety from the factory hydrostatic proof test conducted at room temperature, unless the test pressures are raised in ratio to the loss of strength at operating temperature.
Division 2 Vs. Division 3 and Load-Resistance-Factor Design (LRFD)
As previously mentioned, whenever design practice is envisioned in the oil field, one often assumes linear-elastic-stress analysis when referring to ASME VIII Division 2. However, Division 2 cites many design and analysis methods. ASME VIII Division 3 contains most of the same techniques but with more-stringent requirements for “design pressures generally above 10,000 psi.” Division 3 cites lower design margins and test pressures, seen as beneficial to keeping pressure-vessel-wall thicknesses reasonable. However, these lower values come with tighter controls on material strength and with far more material ductility than Division 2 requires. Thus, the argument made earlier that either Division 2 or Division 3 design methods may be used is a valid one, although one must consider what the actual values of these design margins are. Those specifically listed in the codes are related to pressure vessels alone.
One of the more-accurate analysis methods within Divisions 2 and 3 is LRFD. This technique uses finite-element analysis along with prescribed load factors to verify that a pressure-vessel design has an adequate margin against collapse or rupture. ASME has prescribed tables of load factors for use with LRFD, one set for Division 2 and another for Division 3, established for common pressure-vessel load combinations. The load combinations focus on pressure containment, but can they be applied to pressure vessels with highly stressed load-bearing parts? The oil industry needs to develop its own set of load combinations and load factors for HP/HT and combined load-bearing/pressure-containment situations.
Existing Failure-Assessment Diagram
API 6A and 17D, which are most applicable to wellhead equipment, do not require the designer to address fatigue, only to consider it. However, when designing HP/HT equipment to either ASME VIII Division 2 or Division 3, cyclic loading and fast-fracture failure need to be tested analytically. If an ASME pressure vessel can be shown to fail in a “safe” (leak-before-burst) mode, then S/N fatigue analysis is acceptable to see if cyclic loads will affect design adversely. And if the load’s stresses are kept below a certain limit, infinite cycle life can be inferred (and neglected, as assumed in API 6A design calculations). If not, fracture mechanics is required. Division 2 realizes there is a point at which stresses elevate to a level where leak-before-burst gives way to fast-fracture burst. But this threshold is very dependent on geometry, wall thickness, material toughness, and material yield strength, along with flaw shape and size and the location of the high stress within the geometry. So, to test for this threshold, a fitness-for-service procedure typically used for evaluating existing pressure-vessel hardware is cited as a means to evaluate a hypothetical design situation. This test, commonly referred to as the failure-assessment diagram (FAD), is found in several fitness-for-service codes. The FAD-analysis procedure is illustrated in Fig. 1.
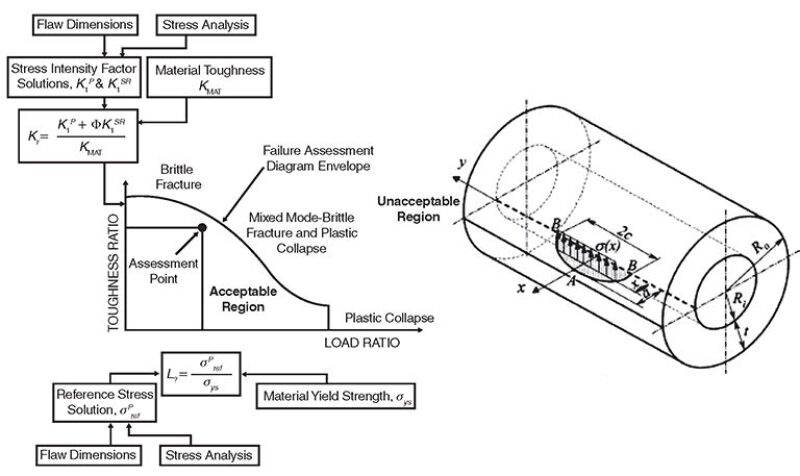
Proposed FAD
The FAD is an assessment tool for looking at an existing part and determining its remaining useful life. It looks at one assessment point at a time. The FAD provides little intuition as to predicting cyclic (dynamic) vs. a static or quasistatic state for a particular design and selected material without a long series of experimental cyclic-loading tests to create a series of cracks to be plotted. To bring cycle count into the FAD process, the use of another fracture-mechanics principle, the Paris law for crack growth, is needed. The tabulated results can be graphed to create a representative S/N curve.
The resulting trends indicate that pressure-vessel size will have the largest effect on cycle count. This can be inferred from the fact that the FAD predicts that a much larger crack size is needed to break through a thicker-walled object than a thinner one. Initial-flaw-size variation has a relatively minor effect on cyclic performance, bunching the curves close together.
Temperature also seems to have a lesser effect because all of the stress values used to define reference stress and stress-intensity factors are based on the same material yield strength, moving proportionally with the temperature. However, there is some movement because of changes in the Paris-law variables. An increase in these values with increased temperature indicates an increase of the crack-growth rate, thereby moving the curve slightly to the left as temperature increases.
This proposed representative S/N curve has its drawbacks. First, the generated curves are only as good as the representative Paris-law information to predict the correlation of cycle count and crack growth. Second, the ratio between the cylinder wall thickness to the crack depth is a critical part of the FAD’s estimation of stress intensity. If a component has an unusually thin cross section in a particular location, the pressure-vessel cylinder used to model it may be too thick to be representative of crack growth and failure at that location (Fig. 2). Third, the FAD process from API 579-1 is a linear-elastic fracture-mechanics model, and the designer is working in the realm of elastic/plastic behavior. Therefore, from the start, the FAD curve may have some level of inaccuracy as to where the critical flaw size occurs. Therefore, as an assessment point edges closer to the demarcation line, one should be skeptical regarding the resulting cyclic-load capacities or the cycle count that can be considered safe.
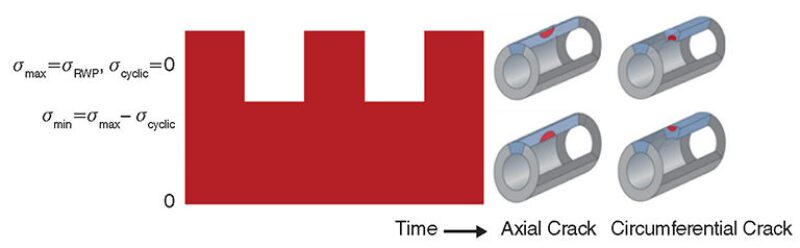
Furthermore, assessment points that fall to the right of the demarcation curve should not necessarily imply that the design has failed or has a limited fatigue life.
The proposed representative S/N curve also depends on a lengthy list of assumptions to cut down the number of variables and to provide a level of uniformity independent of the actual component’s design (see the complete paper for these variables).
This article, written by JPT Technology Editor Chris Carpenter, contains highlights of paper OTC 23943, “Design-Guideline Strategies for High-Pressure/High-Temperature Equipment,” by H. Brian Skeels, Kwok Lun Lee, and Anand Venkatesh, FMC Technologies, prepared for the 2013 Offshore Technology Conference, Houston, 6–9 May. The paper has not been peer reviewed. Copyright 2013 Offshore Technology Conference. Reproduced by permission.
