The Wisdom of Learning Invariant Quantities
It’s remarkable that we ever have an “ordinary day.” If we were to sit down and catalogue all of our experiences—the flavors of our sandwich, the quality of the sunlight, or the texture of our cat’s fur—no day would look like any other. The stew of sensory information would be simply overwhelming.
The only way to make sense of our complicated day-to-day experiences is to focus on the things that don’t change—the invariants, the conserved quantities. Over time, we pick up on these things and use them as anchors or reference points for our sense of reality. Our sandwich tastes different—maybe the bread is stale. The cat doesn’t feel as soft as usual—maybe it needs a bath. It’s beneficial to understand what does not vary in order to make sense of what does.
This is a common theme in physics. Physicists start with a small set of “invariant quantities” such as total energy, total momentum, and (sometimes) total mass. Then they use these invariances to predict the dynamics of a system. “If energy is conserved,” they might say, “when I throw a ball upwards, it will return to my hand with the same speed as when it left.”
But these common-sense rules can be difficult to learn straight from data. On tasks such as video classification, reinforcement learning, or robotic dexterity, machine-learning researchers train neural networks on millions of examples. And yet, even after seeing all of these examples, neural networks don’t learn exact conservation laws. The best they can do is gradually improve their approximations.
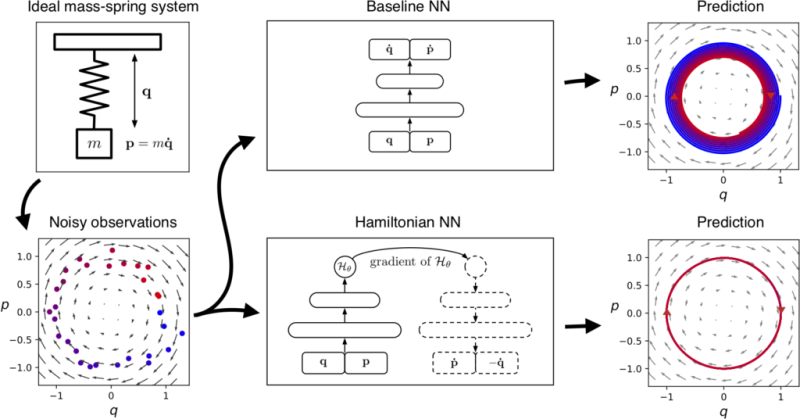
we parameterize it with a neural network and then learn it
directly from data. The variables q and p correspond to
position and momentum coordinates. As there is no friction,
the baseline's inward spiral is due to model errors.
By comparison, the Hamiltonian neural network learns
to exactly conserve an energy-like quantity.
As an example, consider the ideal mass-spring system shown in Fig. 1. Here the total energy of the system is being conserved. More specifically, a quantity proportional to q2+p2q2+p2 is being conserved, where qq is the position and pp is the momentum of the mass. The baseline neural network learns an approximation of this conservation law, and yet the approximation is imperfect enough that a forward simulation of the system drifts slowly to a different energy state. Can we design a model that doesn’t drift?
Hamiltonian Neural Networks
It turns out we can. Drawing inspiration from Hamiltonian mechanics, a branch of physics concerned with conservation laws and invariances, we define Hamiltonian neural networks (HNNs). By construction, these models learn conservation laws from data. We’ll show that they have some major advantages over regular neural networks on a variety of physics problems.
We begin with an equation called the Hamiltonian, which relates the state of a system to some conserved quantity (usually energy) and lets us simulate how the system changes with time. Physicists generally use domain-specific knowledge to find this equation, but here we try a different approach: Instead of crafting Hamiltonians by hand, we parameterize them with neural networks and then learn them directly from data.

