With the recent drop in oil prices, operators are shifting to optimization of existing assets with minimal costs. For mature floods (water, chemical, and CO2), one low-cost optimization strategy is the intelligent adjustment of well-rate targets. While it is easy to identify high-water-cut or high-water-rate producers, it is not obvious to identify which injectors are contributing to oil production or fluid cycling. This makes setting injection targets a guessing game at best without a calibrated reservoir (simulation) model.
However, detailed calibrated reservoir models require simulation expertise, are time-consuming to build, and can even be considered overkill for short-term reservoir management. Reservoir surveillance techniques sidestep this problem by using measured well data combined with simpler models to create a feedback loop that is informative and valuable for reservoir management.
The starting point for any improvement of an ongoing flood is the proper identification of well patterns and reliable pattern metrics. Which patterns have historically outperformed and which have underperformed? How much oil is being recovered from each pattern for each unit of volume injected into the pattern?
Being able to answer these questions with confidence enables target rates to be set that will improve sweep and reduce fluid cycling. And as new production/injection data are collected, rate targets are realigned to ensure that field recovery remains close to optimum.
Streamlines as a Solution
Streamlines, which represent flow from injectors or aquifers to producers, offer a powerful solution to define injector patterns and associated key production metrics. Advances in streamline-based flow modeling since the early 1990s allow streamlines to be traced in 3D, account for complex geological descriptions, include all well geometries, and incorporate a wide range of flow physics. However, applying streamlines for surveillance requires only a subset of these extensions and is much simpler to implement.
Most floods are driven by pressure gradients rather than absolute pressure, and at reservoir conditions, it can be assumed that the fluids are nearly incompressible. This is certainly true for water/polymer/chemical floods. Even CO2 at high pressure behaves like a liquid.
For surveillance purposes, the calculation for the total velocity field needed to trace the streamlines can be significantly simplified. Specifically, the velocity is solved conditioned to a) measured (historical) total injected and produced volumes at the wells; b) a description of the subsurface geology, including faults and flow barriers if available, and if not, a homogenous box can be used; and c) an assumption of in-situ fluid distributions if available, and if not, a uniform saturation distribution will do.
Although these assumptions seem substantial, they are reasonable for surveillance because the primary objective is to identify current well pairs and allocation factors rather than forecasting.
Model Calibration Not Needed
The assumption of fluid incompressibility implies that the past spatial pressure distribution and gradients are immaterial to the solution of the current velocity field, and so streamlines can be extracted for any moment in time without the need to calibrate the model to the past. Using measured historical produced and injected total rates implies that the velocity field will properly reflect the influence of wells relative to each other in terms of production/injection volume and spatial location.
An often overlooked detail is that historical well data implicitly contain information about reservoir connectivity—high injection/production volumes are usually indicative of good pay and support compared with low injection/production volumes. This is the reason why bubble plots are popular among engineers looking for clues to the spatial quality of a reservoir. By using historical measured rates to solve for the current spatial pressure gradients, the resulting velocity field will implicitly reflect such connectivity.
It is possible to add a spatial description of geological properties such as permeability, porosity, or net to gross, etc., as well as transmissibility barriers, such as faults and shale barriers, to further condition the velocity field. Special consideration should be given to flow barriers, as these will radically affect the flow field and tracing of streamlines. Local permeability/porosity modifications, on the other hand, are a lesser factor.
Defining Injection Patterns
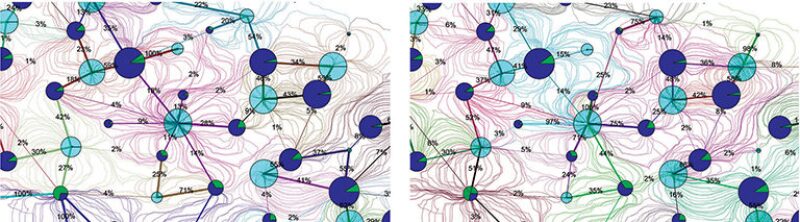
Once the total velocity is known, tracing streamlines from injectors to producers automatically defines patterns and injector/producer pairs. For example, a pattern may be defined as an injector (light blue bubbles displaying injection rates in Fig. 1) and all the producers connected to that injector by streamlines. Alternatively, one can define a pattern as being centered on a producer with associated injectors connected by streamlines. There are usually fewer injectors than producers, and because the goal of a flood is to produce oil by sweeping it with injected fluid toward the producers, centering patterns on injectors has proven to be a good, practical choice.
To extract pattern metrics, it is useful to consider each streamline as being the center of a streamtube carrying a fraction of the total flow rate of the wells to which it is connected. The sum of all the streamlines ending or starting in a well is therefore expected to equal the total flow rate of that well.
Similarly, summing up the rates of the streamlines between any injector/producer pair will quantify the total rate between the well pair (Batycky et al. 2008). That allows estimation of the well allocation factors (WAFs) as the ratio of the total rate of an injector/producer pair to the total well rate of either the injector or producer on either end of the connection (Fig. 1). Furthermore, as production history changes, the streamlines are updated, the WAFs are recomputed, and the patterns evolve through time.
Estimating Pattern Efficiency
With WAFs in hand, it is straightforward to estimate the efficiency of each pattern (injector), which is simply the oil production rate of all the connected producers weighted by the respective producer WAFs and then divided by the water injection rate. In other words, it is possible to associate oil production with an injector (as shown in the left frame of Fig. 2). It should be reiterated that all the calculations are based on historical observed well rates—from the derivation of the streamlines to the final calculation of the WAFs—giving a summary plot of good vs. poor use of injected fluids based on measured data.
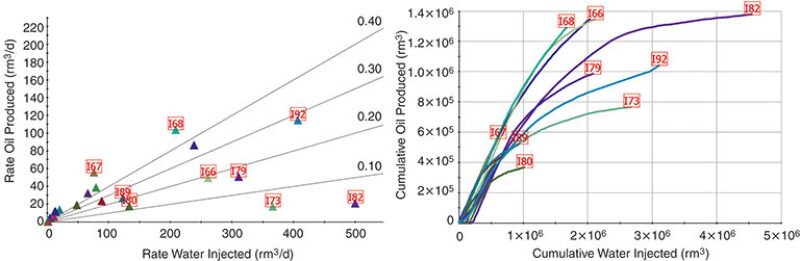
It is also possible to estimate the cumulative oil produced by each pattern (injector) by properly accounting for the changing production rates and WAFs over time (as shown in the right frame of Fig. 2). The plots in Fig. 2 are a powerful diagnostic view of the flood, quantifying the relative efficiency of each pattern historically (right) and currently (left). This is what makes the streamline-based surveillance model so unique and useful.
The final goal is to estimate future well target rates based on the streamline-based pattern metrics. A crucial value is the efficiency of each injector/producer pair, the fraction of oil produced at a well due to a fraction of volume injected by the associated injector. With this information, well rates can be modified to promote higher efficiency connections and demote lower ones (Thiele and Batycky 2006), which amounts to a data-driven approach to improve sweep.
Connection Efficiency
The ability to identify efficient vs. inefficient connections across the injector/producer network—the flux pattern map (Fig. 1)—is what makes streamline-based surveillance unique. Operators know not only which producers are high-water-cut or high-water-rate wells, but now which injectors are contributing to the offset oil production and the efficiency of this contribution. It is a fundamental improvement over the classic rate-target management workflow of predefined fixed patterns and the adjustment of rates to maintain the fixed pattern voidage replacement ratio, which usually does little to promote sweep or avoid fluid cycling.
As well rates and water cuts change over time with updated well-rate targets, the patterns and injector efficiencies will also change. Because there is no assumption about fixed patterns, the streamline-based surveillance metrics should be updated routinely, resulting in new rate targets. Using this feedback loop, the field is nudged toward improved sweep as the good injector-producer connections are promoted and the bad ones are demoted, subject to operational constraints, such as injection volumes and pump capacities.
Operators have shown that using a streamline-based surveillance approach to update rate targets can lead to incremental oil production increases above base decline rates, ranging from 1% to 10% of fieldwide daily oil rate, with minimal effort. In Oman, an operator has seen a 2% increase in the fieldwide oil rate for a heavy oil flood as a result of the intelligent redistribution of injected water. In Austria, OMV has achieved a 30% increase in oil rate for a three-pattern portion of a waterflood (Kornberger and Thiele 2014). The improvements in both cases came at minimal cost.
Summary
Mature pattern floods can benefit significantly from streamline-based surveillance-type workflows, allowing engineers to make decisions quickly and efficiently to manage short-term oil production. Surveillance models are easy to build and can be used in real time, rather than requiring months to assemble and calibrate as with classic reservoir simulation models. The limitation of a surveillance model is that it cannot be used for forecasting, but the wealth of information on injector patterns, well pairs, and allocation factors can be used in a real-time feedback loop to continuously manage the reservoir.
Streamline-based surveillance is an alternative to other surveillance workflows and distinguishes itself by (1) defining patterns automatically from the production/injection data through the use of streamlines that connect injectors and producers; (2) accounting for the dynamic nature of fluid flow and allowing patterns to change in time; (3) extracting per-injector/-producer metrics, such as WAFs and efficiencies, and (4) being applicable to water, CO2, and chemical floods.
References
Batycky, R.P., Thiele, M.R., and Baker, R.O. et al. 2008. Revisiting Reservoir Flood-Surveillance Methods Using Streamlines. SPE Res Eval & Eng 11 (2): 387–394. SPE 95402-PA.
Kornberger M. and Thiele M.R. 2014. Experiences With an Efficient Rate-Management Approach for the 8th Tortonian Reservoir in the Vienna Basin. SPE Res Eval & Eng 17 (2): 165–176. SPE 166393-PA.
Thiele, M.R. and Batycky, R.P. 2006. Using Streamline-Derived Injection Efficiencies for Improved Waterflood Management. SPE Res Eval & Eng 9 (2): 187–196. SPE 84080-PA.

