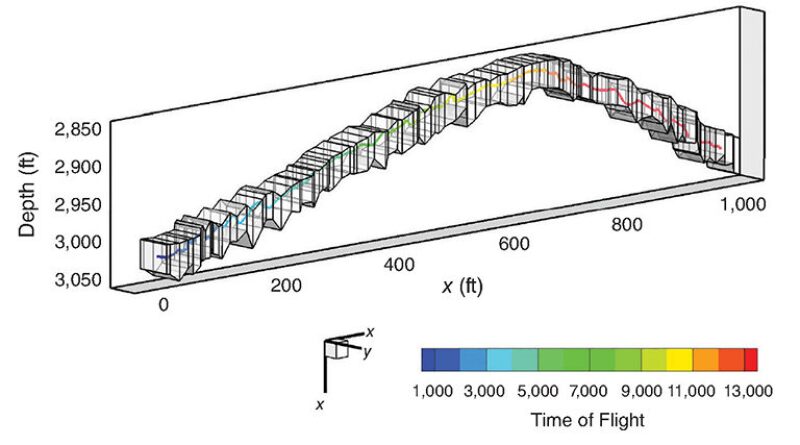
Streamline-based history-matching techniques have provided significant capabilities in integrating field-scale water-cut and tracer data into high-resolution geologic models. However, application of the streamline-based approach for simultaneous integration of water cut and bottomhole pressure (BHP) has been rather limited. In this paper, the authors introduce a novel semianalytic approach to compute the sensitivity of the BHP data with respect to gridblock properties.
Introduction
The streamline-based method has many advantages in terms of computational efficiency and applicability. The main advantage of the streamline-based method is that it is able to calculate parameter sensitivity with a single streamline simulation or post-processing of the grid-based finite-difference simulation results.